Next: In Classical Mechanics Up: Quantum Mechanics Previous: The Laws of Quantum Contents

Particle in a potential.

Let us consider a general situation where there is a particle in a potential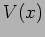

. We have seen that there exist wavefunctions of the form

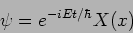$\begin{displaymath} \psi= e^{-i E t/\hbar} X(x) \end{displaymath}$

(20.40)

where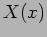

is a solution to the equation

$\begin{displaymath} \frac{\hbar^2}{2m} \frac{d^2 X}{dx^2} = - [E-V(x)] X\,. \end{displaymath}$

(20.41)

What happens if we measure the energy of a particle with such a wavefunction? This is an eigenfunction of the Hamiltonian operator with eigenvalue

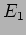. This means that this state has a well defined energy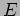

. It is called an energy eigenstate. The probability density of such a state is time independent.

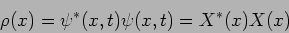$\begin{displaymath} \rho(x) = \psi^*(x,t) \psi (x,t) = X^* (x) X(x) \end{displaymath}$

(20.42)

For this reason a state with a wave function of this form is also called a stationary state.

Next: In Classical Mechanics Up: Quantum Mechanics Previous: The Laws of Quantum Contents

Physics 1st Year 2009-01-06