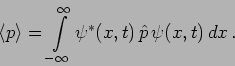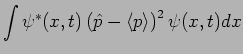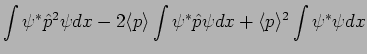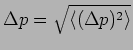In Newtonian Mechanics the trajectory is determined by
solving Newton's equation of motion
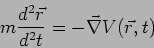 |
(20.1) |
In Quantum Mechanics the wavefunction is governed by
Schrodinger's equation
For a particle free to move only in one dimension along the  axis we
have
axis we
have
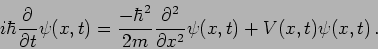 |
(20.3) |
Here we shall only consider time independent potentials 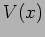 .
Applying the method of separation of variables we take a trial
solution
.
Applying the method of separation of variables we take a trial
solution
whereby the Schrodinger's equation is
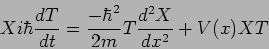 |
(20.5) |
which on dividing by 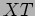 gives
gives
 |
(20.6) |
The first term is a function of  alone whereas the second term is a
function of
alone whereas the second term is a
function of  alone. It is clear that both terms must have a
constant value if they are to be equal for all values of
alone. It is clear that both terms must have a
constant value if they are to be equal for all values of  and
and
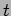 . Denoting this constant as
. Denoting this constant as 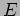 we can write the solution for the time dependent part as
we can write the solution for the time dependent part as
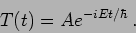 |
(20.7) |
The  dependence has to be determined by solving
dependence has to be determined by solving
![\begin{displaymath}
\frac{\hbar^2}{2m}
\frac{d^2 X}{dx^2} = - [E-V(x)] X\,.
\end{displaymath}](img1565.png) |
(20.8) |
The general solution can be written as
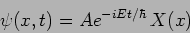 |
(20.9) |
where the  dependence is known and
dependence is known and 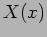 has to be determined from
equation (20.8).
has to be determined from
equation (20.8).
Free particle
The potential 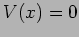 for a free particle. It is straightforward to
verify that
for a free particle. It is straightforward to
verify that
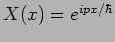 with
with
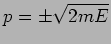 satisfies
equation (20.8).
This gives the solution
satisfies
equation (20.8).
This gives the solution
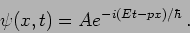 |
(20.10) |
The is a plane wave with angular frequency
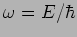 and wave
number
and wave
number 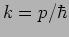 where and
where and 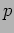 are as yet arbitrary
constant related as
are as yet arbitrary
constant related as 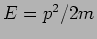 . This gives the wave's dispersion
relation
. This gives the wave's dispersion
relation
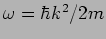 .
.
Here different value of 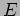 will give different wavefunctions. For
example
will give different wavefunctions. For
example 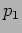 and
and 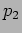 are different constants with
are different constants with
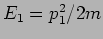 and
and 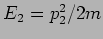 , then
, then
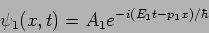 |
(20.11) |
and
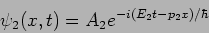 |
(20.12) |
are two different wavefunctions corresponding to two different states
of the particle.
What happens when we make a measurement?
We have already discussed what happens when we measure a particle's
position. In Quantum Mechanics it is not possible to predict
the particle's position. We can only predict probabilities for finding
the particle at different positions. The probability density
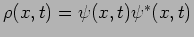 gives the probability
gives the probability 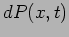 of finding the particle in the interval
of finding the particle in the interval 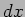 around the point
around the point  to
be
to
be
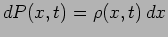 .
But there are other quantities like momentum which we could also
measure. What happens when we measure the momentum?
.
But there are other quantities like momentum which we could also
measure. What happens when we measure the momentum?
InQuantum Mechanics there is a Hermitian Operator
corresponding to every observable dynamical quantity like the
momentum, angular momentum, energy , etc.
What is an operator? An operator 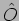 acts on a function
acts on a function
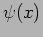 to give another function
to give another function 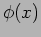 .
.
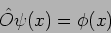 |
(20.15) |
We consider an example where
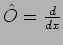
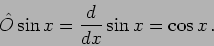 |
(20.16) |
Consider another example where 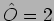 so that
so that
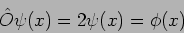 |
(20.17) |
What is a Hermitian operator? We do not go into the definition
here, instead we only state a relevant, important property of a
Hermitian operators. Given an operator 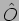 , a function
, a function
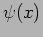 is an eigenfunction of
is an eigenfunction of 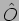 with eigenvalue
with eigenvalue
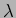 if
if
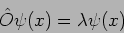 |
(20.18) |
As an example consider
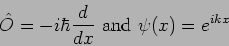 |
(20.19) |
we see that
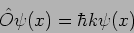 |
(20.20) |
The function 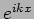 is an eigenfunction of the operator
is an eigenfunction of the operator
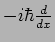 with eigenvalue
with eigenvalue 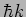 .
As another example for the same operator we consider the
function
.
As another example for the same operator we consider the
function
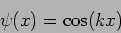 |
(20.21) |
we see that
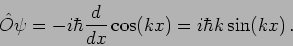 |
(20.22) |
This is not an eigenfunction of the operator.
Hermitian operators are a special kind of operators all of whose
eigenvalues are real.
We present the Hermitian operators corresponding to a few observable
quantities.
Position - x 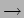 Operator
Operator 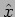
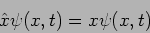 |
(20.23) |
Momentum - p 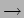 Operator
Operator 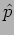
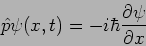 |
(20.24) |
Hamiltonian
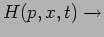 Operator
Operator 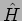
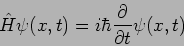 |
(20.25) |
The eigenvalues of the Hamiltonian 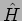 correspond to the
Energy.
correspond to the
Energy.
Let us return to what happens when we make a measurement. Consider a
particle in a state with wavefunction 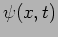 .
We measure its momentum
.
We measure its momentum 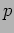 . There are two possibilities
. There are two possibilities
A. If 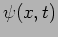 is an eigenfunction of
is an eigenfunction of 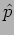 . For
example
. For
example
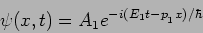 |
(20.26) |
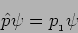 |
(20.27) |
We will get the value 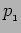 for the momentum The measurement
does not disturb the state and after the measurement the particle
continues to be in the same state with wavefunction
for the momentum The measurement
does not disturb the state and after the measurement the particle
continues to be in the same state with wavefunction 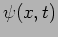 .
.
B. If 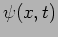 is not an eigenfunction of
is not an eigenfunction of 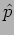 . For
example
. For
example
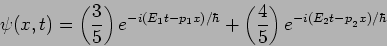 |
(20.28) |
On measuring the momentum we will get either 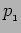 or
or 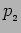 .
The probability of getting
.
The probability of getting
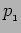 is
is
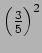 and probability of getting
and probability of getting
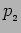 is
is
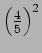 The measurement changes the wavefunction.
The measurement changes the wavefunction.
In case we get 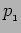 the wavefunction will be changed to
the wavefunction will be changed to
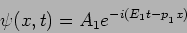 |
(20.29) |
and in case we get 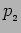 - the wavefunction will be changed to
- the wavefunction will be changed to
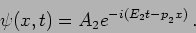 |
(20.30) |
If we measure 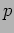 again we shall continue to get the same value in
every successive measurement.
again we shall continue to get the same value in
every successive measurement.
In general, if
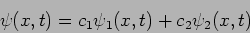 |
(20.31) |
such that
On measuring 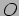
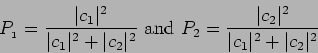 |
(20.33) |
are are probabilities of getting the values 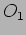 and
and 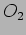 respectively.
We can now interpret the solution
respectively.
We can now interpret the solution
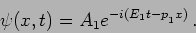 |
(20.34) |
This corresponds to a particle with momentum 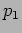 and energy
and energy
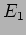 . We will get these value however many times we repeat the
measurement .
. We will get these value however many times we repeat the
measurement .
What happens if we measure the position of a particle whose
wavefunction 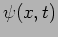 is given by equation (20.34)?
Calculating the probability density
is given by equation (20.34)?
Calculating the probability density
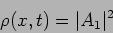 |
(20.35) |
we see that this has no  dependence. The probability of finding the
particle is equal at all points. This wave function has no position
information.
dependence. The probability of finding the
particle is equal at all points. This wave function has no position
information.
![]() ,
, ![]() and
and ![]() with wave functions
with wave functions
![]() ,
, ![]() and
and ![]() respectively.
respectively.
![]() for a free particle. It is straightforward to
verify that
for a free particle. It is straightforward to
verify that
![]() with
with
![]() satisfies
equation (20.8).
This gives the solution
satisfies
equation (20.8).
This gives the solution
![]() and wave
number
and wave
number ![]() where and
where and ![]() are as yet arbitrary
constant related as
are as yet arbitrary
constant related as ![]() . This gives the wave's dispersion
relation
. This gives the wave's dispersion
relation
![]() .
.
![]() will give different wavefunctions. For
example
will give different wavefunctions. For
example ![]() and
and ![]() are different constants with
are different constants with
![]() and
and ![]() , then
, then
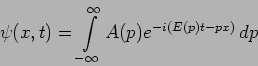
![]() acts on a function
acts on a function
![]() to give another function
to give another function ![]() .
.
![]() Operator
Operator ![]()
![]() .
We measure its momentum
.
We measure its momentum ![]() . There are two possibilities
. There are two possibilities
![]() is an eigenfunction of
is an eigenfunction of ![]() . For
example
. For
example
![]() is not an eigenfunction of
is not an eigenfunction of ![]() . For
example
. For
example
![]() the wavefunction will be changed to
the wavefunction will be changed to
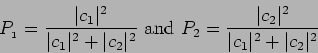
![]() is given by equation (20.34)?
Calculating the probability density
is given by equation (20.34)?
Calculating the probability density
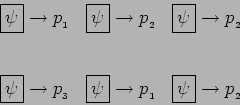
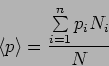
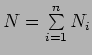 .
In Quantum Mechanics
it is possible to predict this using the particle's wavefunction as
.
In Quantum Mechanics
it is possible to predict this using the particle's wavefunction as