We have seen that the wave function decays exponentially inside a
region where and the decay occurs more rapidly for higher
![]() . In the limit where
. In the limit where
![]() the wavefunction
vanishes at the boundary. We then have
the wavefunction
vanishes at the boundary. We then have
| (20.57) |
| (20.58) |
| (20.59) |
The state with ![]() has the lowest energy
has the lowest energy
| (20.60) |
| (20.61) |
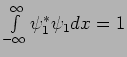 determines
.
determines
.
The ![]() state is the first excited state. It has energy
and its wavefunction (shown in Figure 20.6) is
state is the first excited state. It has energy
and its wavefunction (shown in Figure 20.6) is
| (20.62) |
The wavefunction
| (20.63) |
The energy of the higher excited states increases as ![]() .
Consider a particle that undergoes a transition from the
.
Consider a particle that undergoes a transition from the ![]() state to
the
state to
the ![]() state as shown in Figure 20.7.The particle loses
energy in such a process.
Such a transition may be accompanied by the emission of a photon
(
state as shown in Figure 20.7.The particle loses
energy in such a process.
Such a transition may be accompanied by the emission of a photon
( ![]() ) of frequency
) of frequency
![]() which carries away
the energy lost by the particle.
which carries away
the energy lost by the particle.
It is now possible to fabricate microscopic potential wells using
modern semiconductor technology. This can be achieved
by doping a very small regions of a semiconductor so that an
electron inside the doped region
has a lower potential than the rest of the semiconductor. An
electron trapped inside this potential well will have discrete energy
levels ![]() ,
, ![]() , etc. like the ones calculated here. Such a device is
called a quantum well and photon's are emitted when electron's jump
from a higher to a lower energy level inside the quantum well.
, etc. like the ones calculated here. Such a device is
called a quantum well and photon's are emitted when electron's jump
from a higher to a lower energy level inside the quantum well.