



Next: Particle in a box
Up: Particle in a potential.
Previous: In Classical Mechanics
Contents
Here we shall make a simplification and assume that is
constant over a range of  and it varies in steps as shown in
Figure 20.2 instead of varying smoothly as shown in
Figure 20.1
and it varies in steps as shown in
Figure 20.2 instead of varying smoothly as shown in
Figure 20.1
We calculate the wavefunction of a particle of energy 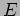 inside a
region of constant potential
inside a
region of constant potential  . We have
. We have
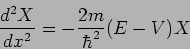 |
(20.45) |
There are two possibilities. The
first possibility, shown in Figure 20.3, is where
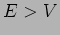 . The particle's momentum inside the potential is
. The particle's momentum inside the potential is
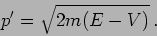 |
(20.46) |
Writing equation (20.45) in terms of this we have
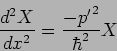 |
(20.47) |
which has a solution
The wave function inside the potential is
![\begin{displaymath}
\psi(x,t) = e^{-iE t/\hbar} \left[
A_1 e^{i p' x/\hbar} + A_2 e^{-i p' x /\hbar} \right]
\end{displaymath}](img1656.png) |
(20.49) |
and for the same particle
outside where 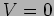 we have
we have
![\begin{displaymath}
\psi(x,t) = e^{-iE t/\hbar} \left[
A_1 e^{i p x/\hbar} + A_2 e^{-i p x /\hbar} \right]
\end{displaymath}](img1657.png) |
(20.50) |
where
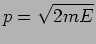 .
We see that the wavefunctions frequency is the same both inside and
outside the potential, whereas the
wave number is different inside the potential (Figure 20.3)
and outside.
The potential is like a change in the refractive index, the
wavelength changes. We shall discuss matching of boundary conditions
later.
.
We see that the wavefunctions frequency is the same both inside and
outside the potential, whereas the
wave number is different inside the potential (Figure 20.3)
and outside.
The potential is like a change in the refractive index, the
wavelength changes. We shall discuss matching of boundary conditions
later.
The second possibility, shown in Figure 20.4 is where 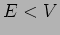 .
.
In classical mechanics the particle is never found in this region as
the momentum is imaginary which is meaningless. Defining
we write equation (20.45) as
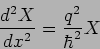 |
(20.52) |
which has solutions
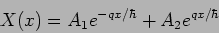 |
(20.53) |
The second solution blows up as 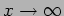 and if the region to
the right extends to infinity then
and if the region to
the right extends to infinity then 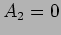 and we have the solution
and we have the solution
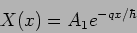 |
(20.54) |
in the region inside the potential. The corresponding wavefunction is
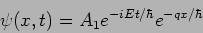 |
(20.55) |
The wave function decays exponentially inside the potential.
There is finite probability of finding the particle in a region 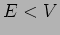 The probability decays exponentially inside the region where
The probability decays exponentially inside the region where 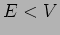 .
The decay rate increases with
.
The decay rate increases with  .
.




Next: Particle in a box
Up: Particle in a potential.
Previous: In Classical Mechanics
Contents
Physics 1st Year
2009-01-06
![]() inside a
region of constant potential
inside a
region of constant potential ![]() . We have
. We have
![]() . The particle's momentum inside the potential is
. The particle's momentum inside the potential is
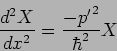
![]() .
.
![]() The probability decays exponentially inside the region where
The probability decays exponentially inside the region where ![]() .
The decay rate increases with
.
The decay rate increases with ![]() .
.