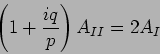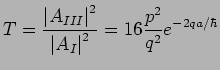Next: Scanning Tunnelling Microscope
Up: Particle in a potential.
Previous: Particle in a box
Contents
A particle of energy 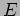 is incident on a step potential of hight
is incident on a step potential of hight
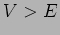 as shown in Figure 20.8.
The step potential extends from
as shown in Figure 20.8.
The step potential extends from 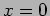 to
to 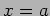 , the potential is zero
on either side of the step.
The particle has wavefunction
, the potential is zero
on either side of the step.
The particle has wavefunction
![\begin{displaymath}
\psi_I(x,t) = e^{-iEt//\hbar} \left[ A_I e^{ i p x/\hbar} +
B_I e^{-ipx/\hbar} \right]
\end{displaymath}](img1694.png) |
(20.64) |
in region 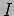 to the left of the step. The
first pat
to the left of the step. The
first pat
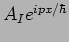 represents the incident particle
ie. travelling along
represents the incident particle
ie. travelling along 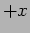 direction and the second part
direction and the second part
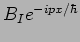 the reflected particle travelling along the
the reflected particle travelling along the
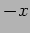 axis.
axis.
In classical mechanics there is no way that the particle can cross
a barrier of height 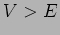 In quantum mechanics the particles's
wave function penetrates inside the step and in region
In quantum mechanics the particles's
wave function penetrates inside the step and in region 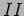 we
have
we
have
![\begin{displaymath}
\psi_{_{II}} (x,t) = e^{-iEt/\hbar} \left[ A_{II}
e^{-qx/\hbar} + B_{II} e^{qx/\hbar}\right]
\end{displaymath}](img1698.png) |
(20.65) |
In region 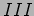 the wave function is
the wave function is
![\begin{displaymath}
\psi_{III} (x,t) = e^{-iEt/\hbar} \left[ A_{III}
e^{ipx/\hbar}+ B_{III}e^{-ipx/\hbar}\right]
\end{displaymath}](img1700.png) |
(20.66) |
where the term
 represents a particle
travelling to the right and
represents a particle
travelling to the right and
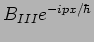 represents a
particle incident from the right. In the situation that we are
analyzing there no particles incident from the right and hence
represents a
particle incident from the right. In the situation that we are
analyzing there no particles incident from the right and hence
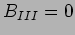 .
.
In quantum mechanics the wave function does not vanish in region
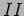 . As shown in Figure 20.8 the incident wave function
decays exponentially in this region , and there is a non-zero
value at the other boundary of the barrier. As a consequence there
is a non-zero wavefunction in region
. As shown in Figure 20.8 the incident wave function
decays exponentially in this region , and there is a non-zero
value at the other boundary of the barrier. As a consequence there
is a non-zero wavefunction in region 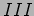 implying that there is
a non-zero probability that the particle penetrates the potential
barrier and gets through to the other side even though its energy
is lower than the height of the barrier. This is known as quantum
tunnelling. It is as if the particle makes a tunnel through the
potential barrier and reaches the other side. The probability that
the incident particle tunnels through to the other side depends on
the relative amplitude of the incident wave in region
implying that there is
a non-zero probability that the particle penetrates the potential
barrier and gets through to the other side even though its energy
is lower than the height of the barrier. This is known as quantum
tunnelling. It is as if the particle makes a tunnel through the
potential barrier and reaches the other side. The probability that
the incident particle tunnels through to the other side depends on
the relative amplitude of the incident wave in region 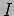 and the
wave in region
and the
wave in region 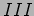 . The relation between these amplitude can be
worked out by matching the boundary conditions at the boundaries
of the potential barrier.
. The relation between these amplitude can be
worked out by matching the boundary conditions at the boundaries
of the potential barrier.
The wave function and its  derivative should both be continuous at
all the boundaries. This is to ensure that the Schrodinger's equation
is satisfied at all points including the boundaries.
derivative should both be continuous at
all the boundaries. This is to ensure that the Schrodinger's equation
is satisfied at all points including the boundaries.
Matching boundary conditions at 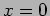 we have
we have
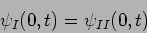 |
(20.67) |
and
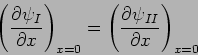 |
(20.68) |
We also assume that the step is very high 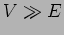 so that
so that
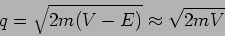 |
(20.69) |
and we also know that
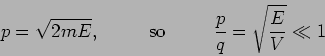 |
(20.70) |
Applying the boundary conditions at 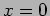 we have
we have
and
The latter condition can be simplified to
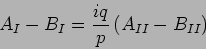 |
(20.73) |
Applying the boundary conditions at 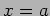 we have
we have
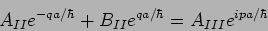 |
(20.74) |
and
![\begin{displaymath}
-q \left[A_{II} e^{-qa/\hbar} - B_{II}e^{qa/\hbar}\right] = ip
A_{III} e^{ipa/\hbar} \,.
\end{displaymath}](img1713.png) |
(20.75) |
The latter condition can be simplified to
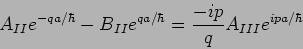 |
(20.76) |
Considering the 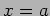 boundary first and using the fact
that
boundary first and using the fact
that 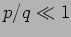 we have
we have
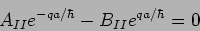 |
(20.77) |
which implies that
Using this in equation (20.74) we have
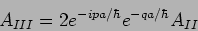 |
(20.79) |
Considering the boundary at 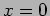 next, we can drop
next, we can drop 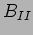 as it is
much smaller than the other terms. Adding equations (20.71)
and (20.73) we have
as it is
much smaller than the other terms. Adding equations (20.71)
and (20.73) we have
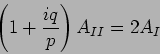 |
(20.80) |
and as 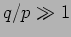 , this gives us
, this gives us
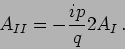 |
(20.81) |
Using this in equation (20.79) we have
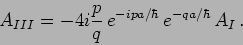 |
(20.82) |
The transmission coefficient
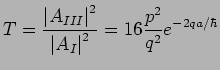 |
|
|
(20.83) |
gives the probability that an incident particle is transmitted through
the potential barrier. This can also be expressed in terms of 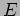 and
and
 as
as
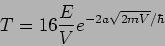 |
(20.84) |
The transmission coefficient drops if either 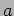 or
or  is increased.
The reflection coefficient
is increased.
The reflection coefficient 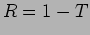 gives the probability that an
incident particle is reflected.
gives the probability that an
incident particle is reflected.




Next: Scanning Tunnelling Microscope
Up: Particle in a potential.
Previous: Particle in a box
Contents
Physics 1st Year
2009-01-06
![]() is incident on a step potential of hight
is incident on a step potential of hight
![]() as shown in Figure 20.8.
The step potential extends from
as shown in Figure 20.8.
The step potential extends from ![]() to
to ![]() , the potential is zero
on either side of the step.
The particle has wavefunction
, the potential is zero
on either side of the step.
The particle has wavefunction
![]() In quantum mechanics the particles's
wave function penetrates inside the step and in region
In quantum mechanics the particles's
wave function penetrates inside the step and in region ![]() we
have
we
have
![]() the wave function is
the wave function is
![]() . As shown in Figure 20.8 the incident wave function
decays exponentially in this region , and there is a non-zero
value at the other boundary of the barrier. As a consequence there
is a non-zero wavefunction in region
. As shown in Figure 20.8 the incident wave function
decays exponentially in this region , and there is a non-zero
value at the other boundary of the barrier. As a consequence there
is a non-zero wavefunction in region ![]() implying that there is
a non-zero probability that the particle penetrates the potential
barrier and gets through to the other side even though its energy
is lower than the height of the barrier. This is known as quantum
tunnelling. It is as if the particle makes a tunnel through the
potential barrier and reaches the other side. The probability that
the incident particle tunnels through to the other side depends on
the relative amplitude of the incident wave in region
implying that there is
a non-zero probability that the particle penetrates the potential
barrier and gets through to the other side even though its energy
is lower than the height of the barrier. This is known as quantum
tunnelling. It is as if the particle makes a tunnel through the
potential barrier and reaches the other side. The probability that
the incident particle tunnels through to the other side depends on
the relative amplitude of the incident wave in region ![]() and the
wave in region
and the
wave in region ![]() . The relation between these amplitude can be
worked out by matching the boundary conditions at the boundaries
of the potential barrier.
. The relation between these amplitude can be
worked out by matching the boundary conditions at the boundaries
of the potential barrier.
![]() derivative should both be continuous at
all the boundaries. This is to ensure that the Schrodinger's equation
is satisfied at all points including the boundaries.
derivative should both be continuous at
all the boundaries. This is to ensure that the Schrodinger's equation
is satisfied at all points including the boundaries.
![]() we have
we have
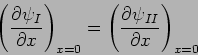
![]() so that
so that
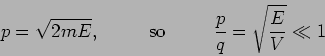
![]() we have
we have
![]() we have
we have
![]() boundary first and using the fact
that
boundary first and using the fact
that ![]() we have
we have
![]() next, we can drop
next, we can drop ![]() as it is
much smaller than the other terms. Adding equations (20.71)
and (20.73) we have
as it is
much smaller than the other terms. Adding equations (20.71)
and (20.73) we have