



Next: About this document ...
Up: Particle in a potential.
Previous: Tunnelling
Contents
The scanning tunnelling microscope (STM) for which a schematic
diagram is shown in Figure 20.9 uses quantum tunnelling
for its functioning. A very narrow tip usually made of tungsten or
gold and of the size of the order of 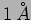 or less is given
a negative bias voltage. The tip scans the surface of the sample
which is given a positive bias. The tip is maintained at a small
distance from the surface as shown in the figure.
Figure 20.10 shows the potential experienced by an
electron respectively in the sample, tip and the vacuum in the gap
between the sample and the tip. As the tip has a negative bias,
and electron in the tip is at a higher potential than in the
sample. As a consequence the electrons will flow from the tip to
the sample setting up a current in the circuit. This is provided
the electrons can tunnel through the potential barrier separating
the tip and the sample. The current in the circuit is proportional
to the tunnelling transmission coefficient
or less is given
a negative bias voltage. The tip scans the surface of the sample
which is given a positive bias. The tip is maintained at a small
distance from the surface as shown in the figure.
Figure 20.10 shows the potential experienced by an
electron respectively in the sample, tip and the vacuum in the gap
between the sample and the tip. As the tip has a negative bias,
and electron in the tip is at a higher potential than in the
sample. As a consequence the electrons will flow from the tip to
the sample setting up a current in the circuit. This is provided
the electrons can tunnel through the potential barrier separating
the tip and the sample. The current in the circuit is proportional
to the tunnelling transmission coefficient 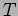 calculated earlier.
This is extremely sensitive to the size of the gap
calculated earlier.
This is extremely sensitive to the size of the gap 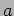 .
.
In the STM the tip is moved across the surface of the sample. The
current in the circuit differs when the tip is placed over
different points on the sample. The tip is moved vertically so
that the current remains constant as it scans across the sample.
This vertical displacement recorded at different points on the
sample gives an image of the surface at the atomic level.
Figure 20.11 shows an STM image of a graphite sample.
Problems
- Consider a particle at time
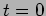 with the wave function
with the wave function
and 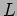 are constants of dimension length.
Given
are constants of dimension length.
Given
![$\int_{-\infty}^{\infty} \exp[-x^2/2] \, dx = \sqrt{2 \pi}$](img1731.png) .
.
- a.
- Determine the normalization constant A.
- b.
- What is the expectation value
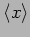 ?
?
- c.
- How much is
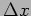 , the uncertainty in
, the uncertainty in  ?
?
- d.
- What is the momentum expectation value
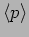 ?
?
- e.
- How much is
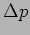 , the uncertainty in
, the uncertainty in 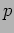 ?
?
- f.
- What happens to the uncertainty in
 and the uncertainty
and the uncertainty
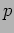 if
if 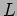 is increased?
is increased?
- d.
- How does the product
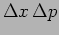 change if
change if 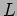 is
varied?
is
varied?
- A free particle of mass
 and energy
and energy 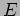 is incident on a
step potential barrier
is incident on a
step potential barrier  . What is the wave function
. What is the wave function 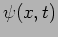 of the particle inside the step potential if (a.) (b.)
of the particle inside the step potential if (a.) (b.) 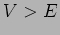 .
.
- A particle of mass
 is confined to
is confined to 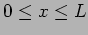 by two
very high step potentials (particle in a box).
by two
very high step potentials (particle in a box).
- a.
- What is the wave function
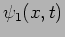 of the particle in
the lowest energy state?
of the particle in
the lowest energy state?
- b.
- What is the wave function
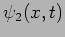 of the particle in
the first excited energy state?
of the particle in
the first excited energy state?
- c.
- For
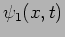 , what are the expectation values
, what are the expectation values
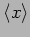 and
and
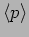 ?
?
- d.
- For
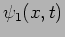 , what are the uncertainties
, what are the uncertainties 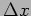 and
and
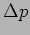 .
.
- An electron trapped in a region of length
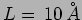 .
(a.)What are the energies of the ground state and the first two
excited states? (b.) An electron in the first excited state
emits radiation and de-excites to the ground state. What is the
wavelength of the emitted radiation?
.
(a.)What are the energies of the ground state and the first two
excited states? (b.) An electron in the first excited state
emits radiation and de-excites to the ground state. What is the
wavelength of the emitted radiation?
- The wave function of a particle confined in a region of length
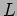 is given to be
is given to be
where 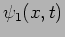 and
and 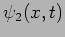 are the wave functions
introduced in Problem 6. What are the possible outcomes and their
probabilities if the energy of the particle is measured? What is the
expectation value of the energy? What is the uncertainty in the
energy?
are the wave functions
introduced in Problem 6. What are the possible outcomes and their
probabilities if the energy of the particle is measured? What is the
expectation value of the energy? What is the uncertainty in the
energy?
- A particle of mass
 and energy
and energy 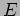 is incident from zero
potential to a step potential
is incident from zero
potential to a step potential  , where
, where 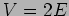 as shown in
Figure 20.12.
as shown in
Figure 20.12.
The
incident, reflected and transmitted wave functions 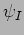 ,
,
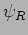 and respectively are
and respectively are
where
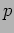 and
and 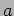 are constants.
are constants.
- a.
- What is the ratio ?
- b.
- Match the boundary conditions at
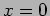 to determine the
ratio
to determine the
ratio 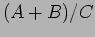 .
.
- c.
- Match the boundary conditions at
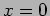 to determine the
ratio
to determine the
ratio 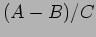 .
.




Next: About this document ...
Up: Particle in a potential.
Previous: Tunnelling
Contents
Physics 1st Year
2009-01-06
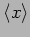 ?
?
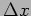 , the uncertainty in
, the uncertainty in  ?
?
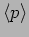 ?
?
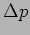 , the uncertainty in
, the uncertainty in 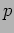 ?
?
 and the uncertainty
and the uncertainty
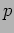 if
if 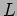 is increased?
is increased?
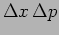 change if
change if 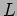 is
varied?
is
varied?
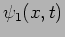 of the particle in
the lowest energy state?
of the particle in
the lowest energy state?
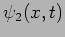 of the particle in
the first excited energy state?
of the particle in
the first excited energy state?
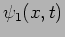 , what are the expectation values
, what are the expectation values
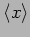 and
and
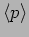 ?
?
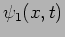 , what are the uncertainties
, what are the uncertainties 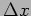 and
and
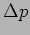 .
.
![]() ,
,
![]() and respectively are
and respectively are
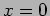 to determine the
ratio
to determine the
ratio 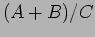 .
.
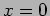 to determine the
ratio
to determine the
ratio 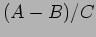 .
.