



Next: Underdamped Oscillations
Up: lect_notes
Previous: LC Oscillator
Contents
Damping usually comes into play whenever we consider motion. We
study the effect of damping on the spring-mass system. The damping
force is assumed to be proportional to the velocity, acting to oppose
the motion. The total force acting on the mass is
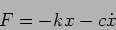 |
(2.1) |
where in addition to the restoring force 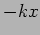 due to the spring we also
have the damping force
due to the spring we also
have the damping force 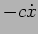 . The equation of motion for the
damped spring mass system is
. The equation of motion for the
damped spring mass system is
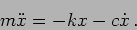 |
(2.2) |
Recasting this in terms of
more convenient coefficients, we have
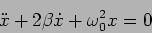 |
(2.3) |
This is a second order homogeneous equation with constant
coefficients. Both 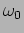 and
and 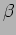 have dimensions
have dimensions
 . Here
. Here 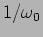 is the time-scale of the oscillations
that would occur if there was no damping, and
is the time-scale of the oscillations
that would occur if there was no damping, and 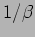 is the time-scale
required for damping to bring any motion to rest. It is clear that the
nature of the motion depends on which time-scale
is the time-scale
required for damping to bring any motion to rest. It is clear that the
nature of the motion depends on which time-scale 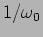 or
or
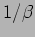 is larger.
is larger.
We proceed to solve equation (2.4) by taking a trial solution
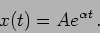 |
(2.4) |
Putting the trial solution into equation (2.4) gives us the
quadratic equation
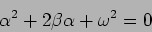 |
(2.5) |
This has two solutions
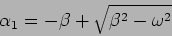 |
(2.6) |
and
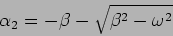 |
(2.7) |
The nature of the solution depends critically on the value of the
damping coefficient 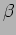 , and the behaviour is quite different
depending on whether
, and the behaviour is quite different
depending on whether
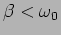 ,
,
 or
or
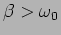 .
.
Subsections




Next: Underdamped Oscillations
Up: lect_notes
Previous: LC Oscillator
Contents
Physics 1st Year
2009-01-06