



Next: Over-damped Oscillations.
Up: The Damped Oscillator.
Previous: The Damped Oscillator.
Contents
We first consider the situation where
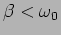 which
is referred to as underdamped. Defining
which
is referred to as underdamped. Defining
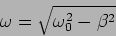 |
(2.8) |
the two roots which are both complex have values
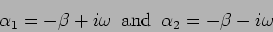 |
(2.9) |
The resulting solution is a superposition of the two roots
![\begin{displaymath}
x(t)=e^{-\beta t} [ A_1 e^{i \omega t} + A_2 e^{-i \omega t} ]
\end{displaymath}](img141.png) |
(2.10) |
where 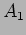 and
and 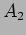 are constants which have to be determined from
the initial conditions. The term
are constants which have to be determined from
the initial conditions. The term
![$[ A_1 e^{i \omega t} + A_1 e^{i
\omega t} ] $](img144.png) is a superposition of
is a superposition of 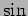 and which can be
written as
and which can be
written as
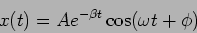 |
(2.11) |
This can also be expressed in the complex notation as
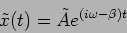 |
(2.12) |
where
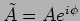 is the complex amplitude which has both
the amplitude and phase information. Figure 2.1 shows the
underdamped motion
is the complex amplitude which has both
the amplitude and phase information. Figure 2.1 shows the
underdamped motion
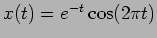 .
.
In all cases damping reduces the frequency of the oscillations
ie.
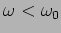 . The main effect of damping is that it
causes the amplitude of the oscillations to decay exponentially with time.
It is often useful to quantify the decay in the amplitude
during the time period of a single oscillation
. The main effect of damping is that it
causes the amplitude of the oscillations to decay exponentially with time.
It is often useful to quantify the decay in the amplitude
during the time period of a single oscillation
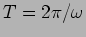 . This
is quantified
by the logarithmic decrement which is defined as
. This
is quantified
by the logarithmic decrement which is defined as
![\begin{displaymath}
\lambda=\ln \left[ \frac{x(t)}{x(t+T)} \right]=\frac{2 \pi \beta}{\omega}
\end{displaymath}](img153.png) |
(2.13) |
Problem 1.: An under-damped oscillator with
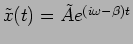 has initial displacement and velocity
has initial displacement and velocity 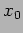 and
and 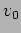 respectively. Calculate
respectively. Calculate 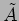 and obtain
and obtain 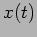 in
terms of the initial conditions.
in
terms of the initial conditions.
Solution:
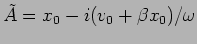 and
and
![$x(t)=e^{-\beta t} \left[ x_0 \cos \omega t + ((v_0 + \beta x_0)/\omega) \,
\sin \omega t \right]$](img156.png) .
.




Next: Over-damped Oscillations.
Up: The Damped Oscillator.
Previous: The Damped Oscillator.
Contents
Physics 1st Year
2009-01-06
![]() . The main effect of damping is that it
causes the amplitude of the oscillations to decay exponentially with time.
It is often useful to quantify the decay in the amplitude
during the time period of a single oscillation
. The main effect of damping is that it
causes the amplitude of the oscillations to decay exponentially with time.
It is often useful to quantify the decay in the amplitude
during the time period of a single oscillation
![]() . This
is quantified
by the logarithmic decrement which is defined as
. This
is quantified
by the logarithmic decrement which is defined as
![\begin{displaymath}
\lambda=\ln \left[ \frac{x(t)}{x(t+T)} \right]=\frac{2 \pi \beta}{\omega}
\end{displaymath}](img153.png)
![]() has initial displacement and velocity
has initial displacement and velocity ![]() and
and ![]() respectively. Calculate
respectively. Calculate ![]() and obtain
and obtain ![]() in
terms of the initial conditions.
in
terms of the initial conditions.
![]() and
and
![]() .
.