



Next: Critical Damping.
Up: The Damped Oscillator.
Previous: Underdamped Oscillations
Contents
This refers to the situation where
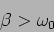 |
(2.14) |
The two roots are
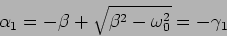 |
(2.15) |
and
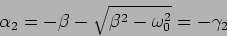 |
(2.16) |
where both
and
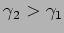 .
The two roots give rise to exponentially decaying solutions, one which
decays faster than the other
.
The two roots give rise to exponentially decaying solutions, one which
decays faster than the other
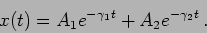 |
(2.17) |
The constants 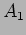 and
and 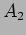 are determined by the initial
conditions. For initial position
are determined by the initial
conditions. For initial position 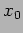 and
velocity
and
velocity 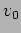 we have
we have
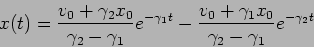 |
(2.18) |
Figure 2.2:
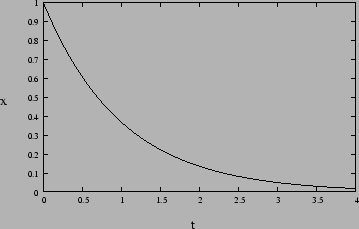 |
The overdamped oscillator does not oscillate. Figure 2.2 shows a
typical situation.
In the situation where
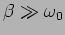
![\begin{displaymath}
\sqrt{\beta^2 - \omega_0^2} = \beta \sqrt{1 -
\frac{\omeg...
... \left[ 1 -
\frac{1}{2}\frac{\omega_0^2}{\beta^2} \right]
\end{displaymath}](img166.png) |
(2.19) |
and we have
and
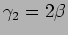 .
.




Next: Critical Damping.
Up: The Damped Oscillator.
Previous: Underdamped Oscillations
Contents
Physics 1st Year
2009-01-06
![]()