



Next: Oscillator with external forcing.
Up: The Damped Oscillator.
Previous: Critical Damping.
Contents
There are two physical effects at play in a damped oscillator. The
first is the damping which tries to bring any motion to a stop. This
operates on a time-scale
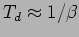 . The restoring force
exerted by the spring tries to make the system oscillate and this
operates on a time-scale
. The restoring force
exerted by the spring tries to make the system oscillate and this
operates on a time-scale
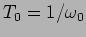 . We have overdamped
oscillations if the damping operates on a shorter time-scale
compared to the
oscillations ie.
. We have overdamped
oscillations if the damping operates on a shorter time-scale
compared to the
oscillations ie. 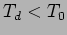 which completely destroys the
oscillatory behaviour.
which completely destroys the
oscillatory behaviour.
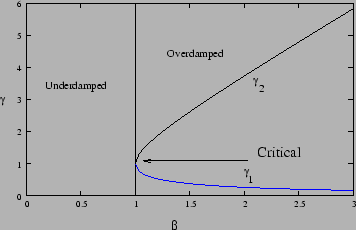
Figure 2.4 shows the behaviour of a damped oscillator under
different combinations of damping and restoring force. The plot is for
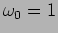 , it can be used for any other value of the natural
frequency by suitably scaling the values of
, it can be used for any other value of the natural
frequency by suitably scaling the values of 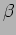 . It shows how the
decay rate for the two exponentially decaying overdamped solutions
varies with
. It shows how the
decay rate for the two exponentially decaying overdamped solutions
varies with 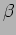 . Note that for one of the modes the decay rate
tends to zero as
. Note that for one of the modes the decay rate
tends to zero as 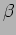 is increased. This indicates that for very
large damping a particle may get stuck at a position away from
equilibrium.
is increased. This indicates that for very
large damping a particle may get stuck at a position away from
equilibrium.
Figure 2.4:
 |
Problems
- Obtain solution (2.20) for critical damping as a limiting case
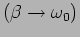 of overdamped solution (2.18).
of overdamped solution (2.18).
- Find out the conditions for the initial
displacement
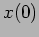 and the initial velocity
and the initial velocity 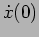 at
at 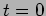 such
that an overdamped oscillator crosses the mean position once in a finite time.
such
that an overdamped oscillator crosses the mean position once in a finite time.
- An under-damped oscillator has a time period of
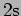 and
the amplitude of oscillation goes down by
and
the amplitude of oscillation goes down by 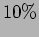 in
one oscillation. [a.] What is the logarithmic decrement
in
one oscillation. [a.] What is the logarithmic decrement 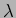 of
the oscillator? [b.] Determine the damping coefficient
of
the oscillator? [b.] Determine the damping coefficient 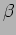 .
[c.] What would be the time period of this oscillator if there was no
damping? [d.] What should be
.
[c.] What would be the time period of this oscillator if there was no
damping? [d.] What should be 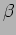 if the time period is to be
increased to
if the time period is to be
increased to 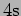 ? ([a.]
? ([a.]
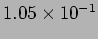 [b.]
[b.]
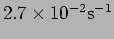 [c.]
[c.]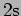 [d.]
[d.]
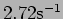
- Two identical under-damped oscillators have damping coefficient
and angular frequency
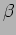 and
and 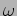 respectively.
At
respectively.
At 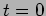 one oscillator is at rest with displacement
one oscillator is at rest with displacement 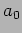 while the
other has velocity
while the
other has velocity 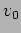 and is at the equilibrium position. What is
the phase difference between these two oscillators. (
and is at the equilibrium position. What is
the phase difference between these two oscillators. (
 )
)
- A door-shutter has a spring which, in the absence of damping,
shuts the door in
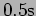 . The problem is that the door bangs
with a speed
. The problem is that the door bangs
with a speed
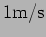 at the instant that
it shuts. A damper with damping
coefficient
at the instant that
it shuts. A damper with damping
coefficient 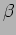 is introduced to ensure that the door shuts
gradually.
What are the time required for the door to shut and
the velocity of the door at the instant it shuts if
is introduced to ensure that the door shuts
gradually.
What are the time required for the door to shut and
the velocity of the door at the instant it shuts if
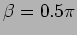 and ? Note that the spring is unstretched
when the door
is shut. (
and ? Note that the spring is unstretched
when the door
is shut. (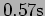 ,
,
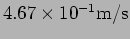 ; ,
; ,
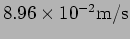 )
)
- An
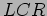 circuit has an inductance
circuit has an inductance
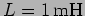 , a
capacitance
, a
capacitance
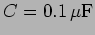 and resistance
and resistance 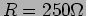 in
series. The capacitor has a voltage
in
series. The capacitor has a voltage 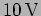 at the instant
at the instant
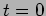 when the circuit is completed. What is the voltage across the
capacitor after
when the circuit is completed. What is the voltage across the
capacitor after
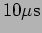 and
and
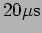 ? (
? (
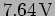 ,
,
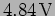 )
)
- A highly damped oscillator with
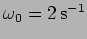 and
and
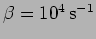 is given an initial displacement of
is given an initial displacement of 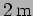 and left at rest. What is the oscillator's position at
and left at rest. What is the oscillator's position at
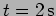 and
and
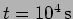 ? (
? (
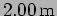 ,
,
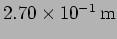 )
)
- A critically damped oscillator with
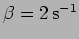 is initially at
is initially at 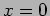 with
velocity
with
velocity
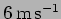 . What is the furthest distance the
oscillator moves from the origin? (
. What is the furthest distance the
oscillator moves from the origin? (
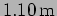 )
)
- A critically damped oscillator
is initially at
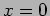 with velocity
with velocity 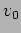 . What is the ratio of the
maximum kinetic energy to the maximum potential energy of this
oscillator? (
. What is the ratio of the
maximum kinetic energy to the maximum potential energy of this
oscillator? (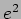 )
)
- An overdamped oscillator is initially at
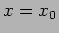 . What initial velocity,
. What initial velocity,
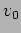 , should be the given to the oscillator that it reaches the mean position
(x=0) in the minimum possible time.
, should be the given to the oscillator that it reaches the mean position
(x=0) in the minimum possible time.
- We have shown that the general solution,
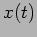 , with two constants can
describe the motion of damped oscillator satisfying given initial conditions.
Show that there does not exist any other solution satisfying the same initial
conditions.
, with two constants can
describe the motion of damped oscillator satisfying given initial conditions.
Show that there does not exist any other solution satisfying the same initial
conditions.




Next: Oscillator with external forcing.
Up: The Damped Oscillator.
Previous: Critical Damping.
Contents
Physics 1st Year
2009-01-06
![]() , it can be used for any other value of the natural
frequency by suitably scaling the values of
, it can be used for any other value of the natural
frequency by suitably scaling the values of ![]() . It shows how the
decay rate for the two exponentially decaying overdamped solutions
varies with
. It shows how the
decay rate for the two exponentially decaying overdamped solutions
varies with ![]() . Note that for one of the modes the decay rate
tends to zero as
. Note that for one of the modes the decay rate
tends to zero as ![]() is increased. This indicates that for very
large damping a particle may get stuck at a position away from
equilibrium.
is increased. This indicates that for very
large damping a particle may get stuck at a position away from
equilibrium.