Critical Damping.

This corresponds to a situation where $\beta = \omega_0$ and the two roots are equal. The governing equation is second order and there still are two independent solutions. The general solution is

$$x(t)=e^{- \beta t} [A_1 + A_2 t]$$ (2.20)

The solution

$$x(t)=x_0 e^{- \beta t} [1 + \beta t]$$ (2.21)

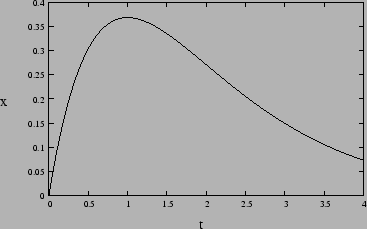
is for an oscillator starting from rest at 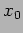$x_0$ while

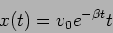$$x(t)=v_0 e^{- \beta t} t$$ (2.22)

is for a particle starting from 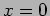$x=0$ with speed 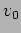$v_0$. Figure 2.3 shows the latter situation.

Figure 2.3: