Sinusoidal Oscillations.

Figure 7.7:

We next consider a situation where a sinusoidal voltage is applied to the dipole oscillator. The dipole is aligned with the $y$ axis (Figure 7.7). The voltage causes the charges to move up and down as

$$y(t) = y_0 \cos(\omega t)$$ (7.6)

with acceleration

$$a(t) =- \omega^2 y_0 \cos(\omega t)\,.$$ (7.7)

producing an electric field

$$E(t)=\frac{q y_0 \omega^2 }{4 \pi \epsilon_0 c^2 r} \, \cos[ \omega (t-r/c)] \, \sin \theta \,.$$ (7.8)

It is often useful and interesting to represent the oscillating charge in terms of other equivalent quantities namely the dipole moment and the current in the circuit. Let us replace the charge $q$ which moves up and down as by two charges, one charge $q/2$ which moves as $y(t)$ and another charge $-q/2$ which moves in exactly the opposite direction as . The electric field produced by the new configuration is exactly the same as that produced by the single charge considered earlier. This allows us to interpret eq. (7.8) in terms of an oscillating dipole

$$d_y(t)=q \, y(t) = d_0 \, \cos(\omega t)$$ (7.9)

which allows us to write eq. (7.8) as

$$E(t)=\frac{-1 }{4 \pi \epsilon_0 c^2 r} \, \ddot{d}_y(t-r/c) \, \sin \theta \,.$$ (7.10)

Returning once more to the dipole oscillator shown in Figure 7.5, we note that the excess electrons which rush from A to B when B has a positive voltage reside at the tip of the wire B. Further, there is an equal excess of positive charge in A which resides at the tip of A. The fact that excess charge resides at the tips of the wire is property of charges on conductors which should be familiar from the study of electrostatics. Now the dipole moment is $d_y(t)= l \, q(t)$ where $l$ is the length of the dipole oscillator and $q(t)$ is the excess charge accumulated at one of the tips. This allows us to write $\ddot{d}_y(t)$ in terms of the current in the wires $I(t)=\dot{q}(t)$ as

$$\ddot{d}_y(t)= l \dot{I}(t)\,.$$ (7.11)

We can then express the electric field produced by the dipole oscillator in terms of the current. This is particularly useful when considering technological applications of the electric dipole oscillator. For a current

$$I(t)=- I \sin(\omega t)$$ (7.12)

the electric field is given by

$$E(t)=\frac{ \omega l I}{4 \pi \epsilon_0 c^2 r} \, \cos[ \omega (t-r/c)] \, \sin \theta \,.$$ (7.13)

where $I$ refers to the peak current in the wire.

We now end the small detour where we discussed how the electric field is related to the dipole moment and the current, and return to our discussion of the electric field predicted by eq. (7.8). We shall restrict our attention to points along the $x$ axis. The electric field of the radiation is in the $y$ direction and has a value

$$E_y(x,t)=\frac{q y_0 \omega^2 }{4 \pi \epsilon_0 c^2 x} \, \cos\left[ \omega t-\left(\frac{\omega}{c}\right) x \right]$$ (7.14)

Let us consider a situation where we are interested in the $x$ dependence of the electric field at a great distance from the emitter. Say we are $1 \, km$ away from the oscillator and we would like to know how the electric field varies at two points which are $1 m$ apart. This situation is shown schematically in Figure 7.7. The point to note is that a small variation in $x$ will make a very small difference to the $1/x$ dependence of the electric field which we can neglect, but the change in the $\cos$ term cannot be neglected. This is because $x$ is multiplied by a factor $\omega/c$ which could be large and a change in $\omega x/c$ would mean a different phase of the oscillation. Thus at large distances the electric field of the radiation can be well described by

$$E_y(x,t)=E \cos\left[ \omega t-k x \right]$$ (7.15)

where the wave number is $k=\omega/c$. This is the familiar sinusoidal plane wave which we have studied in the previous chapter and which can be represented in the complex notation as

$$\tilde{E}_y(x,t)=\tilde{E} e^{i\left[ \omega t-k x \right]}$$ (7.16)

We next calculate the magnetic field . Referring to Figure 7.7 we see that we have $\hat{e}_r=-\hat{i}$. Using this in eq. (7.3) with $\vec{E}=E_y(x,t)\, \hat{j}$ we have

$$\vec{B}(x,t)= \hat{i}\times \vec{E}_y(x,t)/c = \frac{E}{c} \cos(\omega t - kx) \, \hat{k}$$ (7.17)

The magnetic field is perpendicular to $\vec{E}(x,t)$ and its amplitude is a factor $1/c$ smaller than the electric field. The magnetic field oscillates with the same frequency and phase as the electric field.

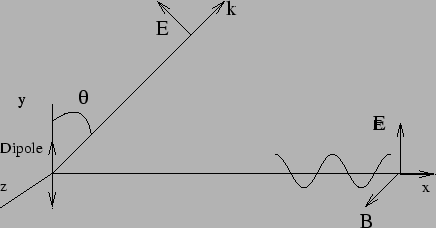
Although our previous discussion was restricted to points along the $x$ axis, the facts which we have learnt about the electric and magnetic fields hold at any position (Figure 7.7). At any point the direction of the electromagnetic wave is radially outwards with wave vector $\hat{k}=k \hat{r}$. The electric and magnetic fields are mutually perpendicular, they are also perpendicular to the wave vector $\hat{k}$.