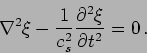Next: Standing Waves
Up: Solving the wave equation
Previous: Plane waves
Contents
We now consider spherically symmetric solutions to the wave equation
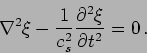 |
(15.40) |
where
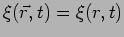 depends only on the distance
depends only on the distance 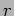 from the
origin. It is now convenient to use the spherical polar coordinates
instead of
from the
origin. It is now convenient to use the spherical polar coordinates
instead of  , and the wave equation becomes
, and the wave equation becomes
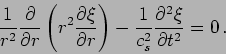 |
(15.41) |
Substituting
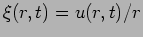 we have
we have
which gives us the wave equation in a single variable 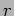 ,
,
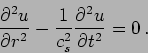 |
(15.43) |
whose solutions are already known. Using these we have
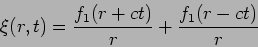 |
(15.44) |
which is the most general spherical wave solution. The first part of
the solution 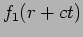 represents a spherical wave travelling
towards the origin and the second part
represents a spherical wave travelling
towards the origin and the second part 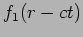 represents a wave
travelling out from the origin as shown in the left and right panels
of Figure 15.7 respectively. In both cases the amplitude
varies as
represents a wave
travelling out from the origin as shown in the left and right panels
of Figure 15.7 respectively. In both cases the amplitude
varies as 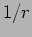 and the solution is singular at
and the solution is singular at 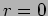 .
.
Figure 15.7:
Spherical waves
|
|




Next: Standing Waves
Up: Solving the wave equation
Previous: Plane waves
Contents
Physics 1st Year
2009-01-06