



Next: Polarization
Up: Solving the wave equation
Previous: Spherical waves
Contents
We consider a stretched string of length 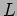 as shown in
Figure 15.8. The string is plucked and left to vibrate. In
this case we have a transverse wave where
as shown in
Figure 15.8. The string is plucked and left to vibrate. In
this case we have a transverse wave where 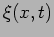 the
displacement of the string is perpendicular to the direction of the
string which is along the
the
displacement of the string is perpendicular to the direction of the
string which is along the  axis.
axis.
Figure 15.8:
A string fixed at the ends
|
|
As we have seen in the earlier section that the evolution of
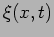 is governed by the wave equation,
is governed by the wave equation,
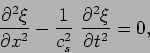 |
(15.45) |
where
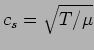 . Here
. Here 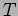 is the tension in the string
and
is the tension in the string
and 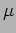 is the mass per unit length of the string. The two ends
of the string are fixed. This imposes the boundary conditions
is the mass per unit length of the string. The two ends
of the string are fixed. This imposes the boundary conditions
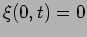 and
and 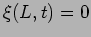 . We could proceed by taking the
general form of the solution and imposing the boundary conditions.
Instead of doing this we proceed to introduce a different method
of solving the wave equation. We take a trial solution of the
form,
. We could proceed by taking the
general form of the solution and imposing the boundary conditions.
Instead of doing this we proceed to introduce a different method
of solving the wave equation. We take a trial solution of the
form,
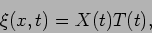 |
(15.46) |
ie. 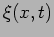 is the product of two functions, the function
is the product of two functions, the function
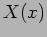 depends only on
depends only on  and the function
and the function 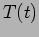 depends only on
depends only on
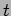 . This is referred to as the separation of variables. The wave
equation now reads,
. This is referred to as the separation of variables. The wave
equation now reads,
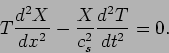 |
(15.47) |
We divide this equation by 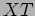 , which gives,
, which gives,
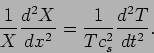 |
(15.48) |
The left hand side of this equation is a function of  alone
whereas the right hand side is a function of
alone
whereas the right hand side is a function of 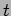 alone. This
implies that each of these two should be separately equal to a
constant ie.
alone. This
implies that each of these two should be separately equal to a
constant ie.
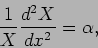 |
(15.49) |
and
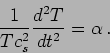 |
(15.50) |
Let us first consider the solution to 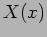 . These are of the
form,
. These are of the
form,
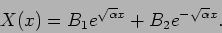 |
(15.51) |
In the situation where  , it is not possible to
simultaneously satisfy the two boundary condition that
, it is not possible to
simultaneously satisfy the two boundary condition that
 and
and 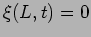 . We therefore consider
. We therefore consider 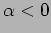 and write it as,
and write it as,
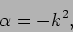 |
(15.52) |
and the equation governing 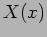 is
is
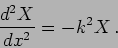 |
(15.53) |
This is the familiar differential equation of a Simple Harmonic
Oscillator whose solution is,
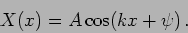 |
(15.54) |
The boundary condition 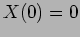 implies that
implies that
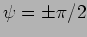 whereby
whereby
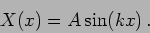 |
(15.55) |
The boundary condition 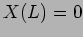 is satisfied only if,
is satisfied only if,
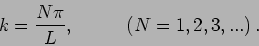 |
(15.56) |
We see that there are a large number of possible solutions, one
corresponding to each value of the integer 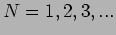 . Let us
next consider the time dependence which is governed by,
. Let us
next consider the time dependence which is governed by,
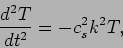 |
(15.57) |
which has a solution,
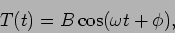 |
(15.58) |
where 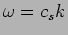 . Combining
. Combining  and
and 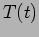 we obtain the
solution,
we obtain the
solution,
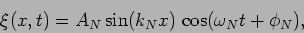 |
(15.59) |
corresponding to each possible value of the integer 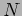 . These are
standing waves and each value of
. These are
standing waves and each value of 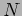 defines a different
mode of the standing wave. The solution with
defines a different
mode of the standing wave. The solution with 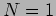 is called the
fundamental mode or first harmonic. We have,
is called the
fundamental mode or first harmonic. We have,
which is shown in the left panel of Figure 15.9. The fundamental
mode has
wavelength 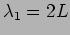 and frequency
and frequency 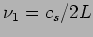 .
.
Figure 15.9:
Standing wave modes: 1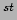 and 2
and 2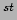 harmonics
harmonics
|
The second harmonic,
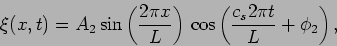 |
(15.61) |
which is shown in the right panel of Figure 15.9 has wavelength
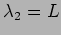 and
frequency
and
frequency 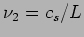 . The higher harmonics have wavelengths
. The higher harmonics have wavelengths
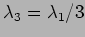 ,
,
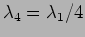 ,
,
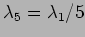 and frequencies
and frequencies 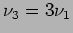 ,
, 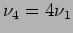 ,
respectively.
,
respectively.
Each standing wave is a superposition of a left travelling and a
right travelling wave. For example,
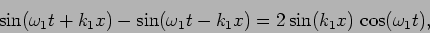 |
(15.62) |
gives the fundamental mode. At all times the left travelling and write
travelling waves exactly cancel at 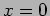 and
and 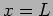 .
.
Figure 15.10:
Arbitrary travelling wave in a string
|
|
Any arbitrary disturbance of the string can be expressed as a sum of
standing waves
The resultant disturbance will in general not be a standing wave but
will travel along the string as shown in Figure 15.10.
Question : If a string which is fixed at both the ends is
plucked at an arbitrary point then which of the modes will not be
excited?
Answer : Read about Young-Helmholtz law.
Problems
- Consider the wave equations
- a.
- What is the dispersion relation for this wave equation?
- b.
- Calculate the phase velocity and the group velocity.
- c.
- Analyze the behaviour when and
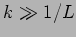
- For the wave equation given below (where
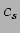 is a
constant)
is a
constant)
- a.
- What is the speed of a travelling wave solution propagating
along the
 axis?
axis?
- b.
- What is the speed of a travelling wave solution propagating
along the
 axis?
axis?
- c.
- For what value of
 is the travelling wave given below a
solution of the wave equation given above?
is the travelling wave given below a
solution of the wave equation given above?
- d.
- What is the speed of the travelling wave given above ?
- Consider the longitudinal disturbance
inside an elastic rod where
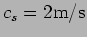 .
.
- a.
- Plot the disturbance as a function of
 .
.
- b.
- What is
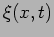 if the disturbance is a travelling wave
moving along
if the disturbance is a travelling wave
moving along 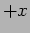 ?
?
- c.
- Plot the disturbance as a function of
 at
at 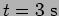 .
.
- Which of the following are travelling waves? If yes, what
is the speed?
- a.
-
![$\xi(x,t)=\sin^2 [ \pi (a x + b t)]$](img1317.png) b.
b.
![$\xi(x,t)=\sin [ \pi (a x + b t)^2]$](img1318.png)
- c.
-
![$\xi(x,t)=\sin^2 [ \pi (a x^2 + b t)]$](img1319.png) d.
d.
![$\xi(x,t)=e^{-[a x^2 + b t^2 + 2 \sqrt{a b} x t]}$](img1320.png)
- e.
-
![$\xi(\vec{r},t)=e^{-[a x + b y- t]^2/L^2}$](img1321.png)
- Consider a spherical wave
![$\xi(r,t)=a \sin[k(r-c_s t)]/r$](img1322.png) with
with
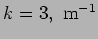 and
and
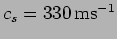 .
.
- a.
- What is the frequency of this wave ?
- b.
- How much does the amplitude of this wave change over
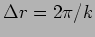 ?
?
- c.
- In which direction does this wave propagate?
- A longitudinal travelling wave
passes through a long steel rod for which
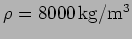 and
and
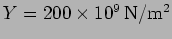 .
.
- a.
- At which point is the displacement maximum at
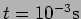 ?
?
- b.
- Plot the displacement at
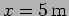 as a function of
time.
as a function of
time.
- c.
- Plot the velocity of the steel at
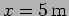 as a
function of time.
as a
function of time.
- d.
- When is the velocity of the steel zero at
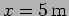 ?
?
- Consider a longitudinal wave
in a steel rod of length
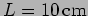 .
.
- a.
- What are the values of the angular frequencies
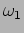 and
and 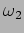 of the fundamental mode and the second harmonic
respectively ?
of the fundamental mode and the second harmonic
respectively ?
- b.
- After what time period does the whole displacement profile
repeat?
- Consider a longitudinal standing wave
in a steel rod of length
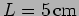 .
.
- a.
- What is the instantaneous kinetic energy per unit volume
at
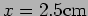 ?
?
- b.
- What is the instantaneous potential energy per unit volume
at
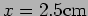 ?
?
- c.
- What is the time averaged kinetic energy per unit volume
at
?
- d.
- What is the time averaged potential energy per unit volume
at
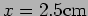 ?
?
- Two steel rods, one
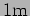 and another
longer are both vibrating in the fundamental mode of longitudinal
standing waves. What is the time period of the beats that will be
produced?
and another
longer are both vibrating in the fundamental mode of longitudinal
standing waves. What is the time period of the beats that will be
produced?
- Write the three dimensional Laplacian operator of equation
(15.40) in spherical polar co-ordinates, and hence obtain
the equation (15.41).




Next: Polarization
Up: Solving the wave equation
Previous: Spherical waves
Contents
Physics 1st Year
2009-01-06
![]() is governed by the wave equation,
is governed by the wave equation,
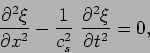
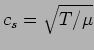 . Here
. Here 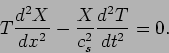
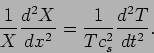
![]() alone
whereas the right hand side is a function of
alone
whereas the right hand side is a function of ![]() alone. This
implies that each of these two should be separately equal to a
constant ie.
alone. This
implies that each of these two should be separately equal to a
constant ie.
![\begin{displaymath}\left[ \nabla^2 - \frac{1}{c^2} \frac{\partial^2}{\partial t^2}
\right] \psi(\vec{r},t)=\frac{1}{L^2} \psi(\vec{r},t)\end{displaymath}](img1309.png)
![\begin{displaymath}\left[ 4 \frac{\partial^2}{\partial x^2}+ 9
\frac{\partial^2...
...c_s^2}\frac{\partial^2}{\partial t^2} \right]
\xi(\vec{r},t)=0\end{displaymath}](img1312.png)