



Next: Spherical waves
Up: Solving the wave equation
Previous: Solving the wave equation
Contents
We consider a disturbance which depends on only one position variable
 . For example
. For example  could be along the length of the beam. We have
the wave equation
could be along the length of the beam. We have
the wave equation
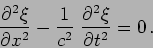 |
(15.30) |
In solving the wave equation it is convenient to introduce two new
variables
We can represent 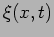 as a function of
as a function of 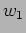 and
and 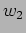 i.e.
i.e.
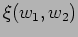
Also
Similarly
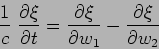 |
(15.31) |
Using these the wave equation becomes
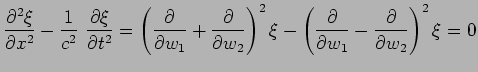 |
|
|
(15.32) |
which gives us the condition
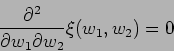 |
(15.33) |
Possible solutions:-
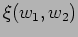 = Constant ( not of interest )
= Constant ( not of interest )
-
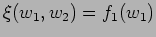 (function of
(function of 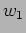 alone.)
alone.)
-
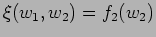 (function of
(function of 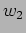 alone.)
alone.)
Any linear superposition of 2 and 3 above is also a solution.
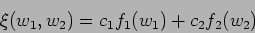 |
(15.34) |
To physically interpret these solutions we revert back to 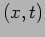 .
.
Let us first consider solution 2 i.e. any arbitrary function of 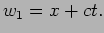
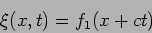 |
(15.35) |
At 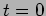 we have
we have
at 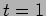 we have
we have
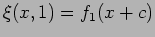 i.e the origin x =0 has
now shifted to
i.e the origin x =0 has
now shifted to 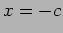 .
and at
.
and at 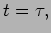 the origin shift to .
The form of the disturbance remains unchanged and the disturbance
propagates to the left i.e. along the
the origin shift to .
The form of the disturbance remains unchanged and the disturbance
propagates to the left i.e. along the 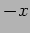 direction with speed
direction with speed 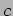 as shown in the left panel of Figure 15.6.
as shown in the left panel of Figure 15.6.
Figure 15.6:
A left moving wave and a right moving wave
|
Similarly, the solution 3 corresponds to a right travelling wave
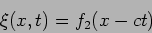 |
(15.37) |
which propagates along with speed 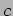 as shown in the right panel
of Figure 15.6
as shown in the right panel
of Figure 15.6
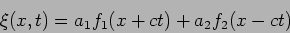 |
(15.38) |
Any arbitrary combination of a left travelling solution and a right
travelling solution is also a solution to the wave equation
The value of 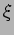 is constant on planes perpendicular to the
is constant on planes perpendicular to the  axis
and these solutions are plane wave solutions. The sinusoidal plane
wave
axis
and these solutions are plane wave solutions. The sinusoidal plane
wave
![\begin{displaymath}
\xi(x,t)=a \cos[k (x-c t) ]
\end{displaymath}](img1247.png) |
(15.39) |
that we have studied earlier is a special case of the more general
plane wave solution.




Next: Spherical waves
Up: Solving the wave equation
Previous: Solving the wave equation
Contents
Physics 1st Year
2009-01-06
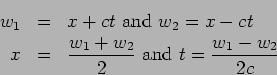
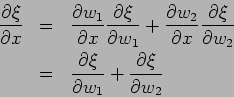
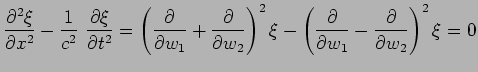
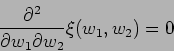
![]()
![]() is constant on planes perpendicular to the
is constant on planes perpendicular to the ![]() axis
and these solutions are plane wave solutions. The sinusoidal plane
wave
axis
and these solutions are plane wave solutions. The sinusoidal plane
wave