Angular resolution

Figure 12.6: Light from two distant sources incident on single slit and their images

We consider a situation where the light from two distant sources is incident on a slit of dimension $D$. The sources are at an angular separation $\Delta \theta$ as shown in Figure 12.6. The light from the two sources is focused onto a screen. In the absence of diffraction the image of each source would be distinct point on the screen. The two images are shown as A and B respectively in Figure 12.6.

Figure 12.7: The Rayleigh criterion for resolution

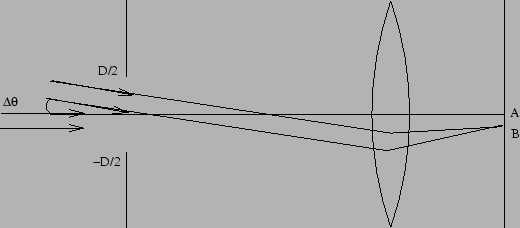
In reality we shall get the superposition of the diffraction patterns produced by the two sources as shown in Figure 12.7. The two diffraction patterns are centered on the positions A and B respectively where we expect the geometrical image. In case the angular separation $\Delta \theta$ is very small the two diffraction patterns will have a significant overlap. In such a situation it will not possible to make out that there are two sources as it will appear that there is a single source. Two sources at such small angular separations are said to be unresolved. The two sources are said to be resolved if their diffraction patterns do not have a significant overlap and it is possible to make out that there are two sources and not one. What is the smallest angle $\Delta \theta$ for which it is possible to make out that there are two sources and not one?

Lord Rayleigh had proposed a criterion that the smallest separation at which it is possible to distinguish two diffraction patterns is when the maximum of one coincides with the minimum of the other (Figure 12.7). It follows that two sources are resolved if their angular separation satisfies

$$\Delta \theta \ge \frac{\lambda}{D}$$ (12.11)

The smallest angular separation $\Delta \theta$ at which two sources are resolved is referred to as the ``angular resolution'' of the aperture. A slit of dimension $D$ has an angular resolution of $\lambda/D$.

Figure 12.8: Circular aperture diffraction pattern

A circular aperture produces a circular diffraction pattern as shown in the Figure 12.8. The mathematical form is a little more complicated than the $\mbox{sinc }$ function which appears when we have a rectangular aperture, but it is qualitatively similar. The first minima is at an angle $\theta = 1.22 \, \lambda/D$ where $D$ is the diameter of the aperture. It then follows that the ``angular resolution'' of a circular aperture is $1.22 \lambda/D$. When a telescope of diameter D is used to observe a star, the image of the star is basically the diffraction pattern corresponding to the circular aperture of the telescope. Suppose there are two stars very close in the sky, what is the minimum angular separation at which it will be possible to distinguish the two stars? It is clear from our earlier discussion that the two stars should be at least $1.22 \lambda/D$ apart in angle, other they will not be resolved. The Figure 12.9 shows not resolved, barely resolved and well resolved cases for a circular aperture.

Figure 12.9: Not resolved, barely resolved and well resolved cases

Diffraction determines the angular resolution of any imaging instrument. This is typically of the order of $\lambda/D$ where $D$ is the size of the instrument's aperture.