



Next: Energy.
Up: Oscillations
Previous: Simple Harmonic Oscillators SHO
Contents
Complex number provide are very useful in representing
oscillations. The amplitude and phase of the oscillation can be
combined into a single complex number which we shall refer to as the
complex amplitude
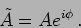 |
(1.6) |
Note that we have introduced the symbol
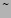 (tilde) to denote
complex numbers. The property that
(tilde) to denote
complex numbers. The property that
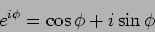 |
(1.7) |
allows us to represent any oscillating quantity
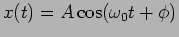 as the real part of the complex number
as the real part of the complex number
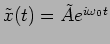 ,
,
![\begin{displaymath}
\tilde{x}(t)= A e^{i (\omega_0t + \phi)}= A [
\cos (\omega_0t + \phi) + i \sin (\omega_0t + \phi)] \,.
\end{displaymath}](img42.png) |
(1.8) |
We calculate the velocity 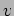 in the complex representation
in the complex representation
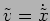 . which gives us
. which gives us
Taking only the real part we calculate the particle's velocity
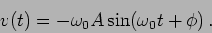 |
(1.10) |
The complex representation is a
very powerful tool which, as we shall see later, allows us to deal
with oscillating quantities in a very elegant fashion.
Problem 3: A SHO has position 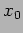 and velocity at the
initial time
and velocity at the
initial time 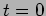 . Calculate the complex amplitude
. Calculate the complex amplitude 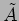 in terms
of the initial conditions and use this to determine the particle's
position
in terms
of the initial conditions and use this to determine the particle's
position 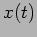 at a later time
at a later time 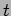 .
.
Solution The initial conditions tell us that
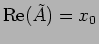 and
and
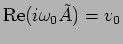 . Hence
. Hence
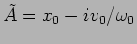 which implies that
which implies that
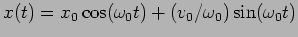 .
.




Next: Energy.
Up: Oscillations
Previous: Simple Harmonic Oscillators SHO
Contents
Physics 1st Year
2009-01-06
![]() in the complex representation
in the complex representation
![]() . which gives us
. which gives us