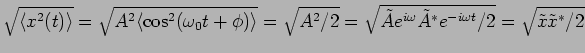 |
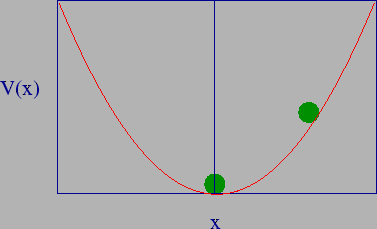
In a spring-mass system the particle has a potential energy
as shown in Figure 1.4.
This energy is stored in the spring when it is either compressed or
stretched. The potential
energy of the system
In a spring-mass system the total energy oscillates between the
potential energy of the spring (![]() ) and the kinetic energy of the
mass (
) and the kinetic energy of the
mass (![]() ).
The total energy
).
The total energy ![]() has a value
which
remains constant.
has a value
which
remains constant.
The average value of an oscillating quantity is often of
interest. We denote the time average of any quantity ![]() using
using
![]() which is defined as
which is defined as
It is very useful to remember that
![]() . This can be easily verified by noting that
the values
. This can be easily verified by noting that
the values
![]() are bound between
are bound between ![]() and
and
![]() . We use this to calculate the average kinetic and potential
energies both of which have the same values
. We use this to calculate the average kinetic and potential
energies both of which have the same values
The average kinetic and potential energies, and the total energy are
all
very conveniently expressed in the complex representation as
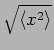 is useful in quantifying the amplitude of
oscillation. Verify that the rms. displacement is
is useful in quantifying the amplitude of
oscillation. Verify that the rms. displacement is
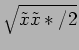 .
.