



Next: Complex Representation.
Up: Oscillations
Previous: Oscillations
Contents
Figure 1.1:
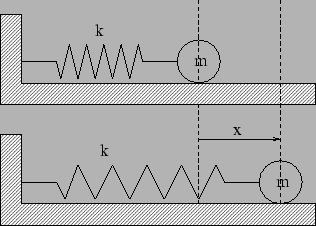 |
We consider the spring-mass system shown in Figure 1.1. A
massless spring, one of whose ends is fixed has its other attached to
a particle of mass  which is free to move. We choose the origin
which is free to move. We choose the origin
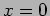 for the particle's motion at the position where the spring is
unstretched. The particle is in stable equilibrium at this position
and
it will continue to remain there if left at rest. We are interested in
a situation where the particle is disturbed from equilibrium.
The particle experiences a restoring force from the
spring if it is either stretched or compressed. The spring is assumed
to be elastic which means that it follows Hooke's law where the force
is proportional to the displacement
for the particle's motion at the position where the spring is
unstretched. The particle is in stable equilibrium at this position
and
it will continue to remain there if left at rest. We are interested in
a situation where the particle is disturbed from equilibrium.
The particle experiences a restoring force from the
spring if it is either stretched or compressed. The spring is assumed
to be elastic which means that it follows Hooke's law where the force
is proportional to the displacement 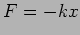 with spring constant
with spring constant
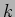 .
.
The particle's equation of motion is
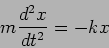 |
(1.1) |
which can be written as
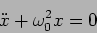 |
(1.2) |
where the dots  denote time derivatives and
denote time derivatives and
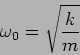 |
(1.3) |
It is straightforward to check that
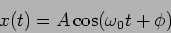 |
(1.4) |
is a solution to eq. (1.4).
We see that the particle performs sinusoidal oscillations around the
equilibrium position when it is disturbed from equilibrium. The
angular frequency 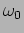 of the oscillation depends on the
intrinsic properties of the oscillator. It determines the time period
of the oscillation depends on the
intrinsic properties of the oscillator. It determines the time period
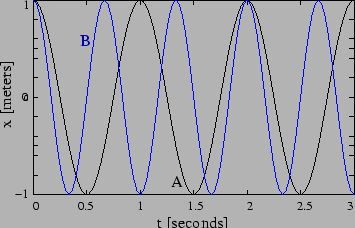
and the frequency 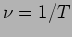 of the oscillation. Figure 1.2
shows oscillations for two different values of
of the oscillation. Figure 1.2
shows oscillations for two different values of 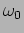 .
.
Problem 1: What are the values of 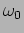 for the oscillations
shown in Figure 1.2? What are the corresponding spring
constant
for the oscillations
shown in Figure 1.2? What are the corresponding spring
constant 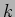 values if
?
values if
?
Solution: For A
and
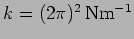 ; For B
; For B
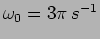 and
and
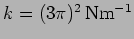
Figure 1.2:
 |
The amplitude 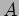 and phase
and phase 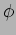 are determined by the initial
conditions. Two initial conditions are needed to completely specify a
solution. This follows from the fact that the governing equation
(1.2) is a second order differential equation. The initial
conditions can be specified in a variety of ways, fixing the values
of
are determined by the initial
conditions. Two initial conditions are needed to completely specify a
solution. This follows from the fact that the governing equation
(1.2) is a second order differential equation. The initial
conditions can be specified in a variety of ways, fixing the values
of 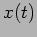 and
and 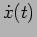 at
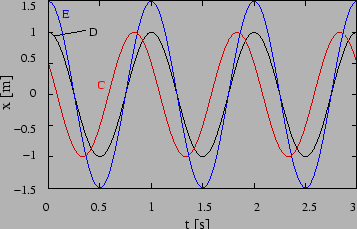
at 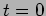 is a possibility. Figure
1.3 shows oscillations with different amplitudes and
phases.
is a possibility. Figure
1.3 shows oscillations with different amplitudes and
phases.
Problem 2: What are the amplitude and phase of the oscillations
shown in Figure 1.3?
Solution: For C, A=1 and 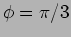 ; For D, A=1 and
; For D, A=1 and
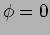 ; For E, A=1.5 and
; For E, A=1.5 and 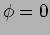 ;
;
Figure 1.3:
 |




Next: Complex Representation.
Up: Oscillations
Previous: Oscillations
Contents
Physics 1st Year
2009-01-06

![]() of the oscillation depends on the
intrinsic properties of the oscillator. It determines the time period
of the oscillation depends on the
intrinsic properties of the oscillator. It determines the time period
![]() and phase
and phase ![]() are determined by the initial
conditions. Two initial conditions are needed to completely specify a
solution. This follows from the fact that the governing equation
(1.2) is a second order differential equation. The initial
conditions can be specified in a variety of ways, fixing the values
of
are determined by the initial
conditions. Two initial conditions are needed to completely specify a
solution. This follows from the fact that the governing equation
(1.2) is a second order differential equation. The initial
conditions can be specified in a variety of ways, fixing the values
of ![]() and
and ![]() at
at ![]() is a possibility. Figure
1.3 shows oscillations with different amplitudes and
phases.
is a possibility. Figure
1.3 shows oscillations with different amplitudes and
phases.
![]() ; For D, A=1 and
; For D, A=1 and
![]() ; For E, A=1.5 and
; For E, A=1.5 and ![]() ;
;