



Next: Electromagnetic Waves.
Up: Sinusoidal Waves.
Previous: Waves in three dimensions.
Contents
Let us now discuss how to describe a sinusoidal plane wave in an
arbitrary direction denoted by the unit vector 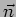 .
A wave propagating along the
.
A wave propagating along the 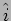 direction can be written as
direction can be written as
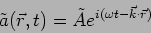 |
(6.13) |
where
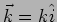 is called the wave vector. Note that
is called the wave vector. Note that 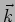 is
different from
is
different from 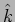 which is the unit vector along the
which is the unit vector along the 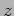 direction. It is now obvious that a wave along an arbitrary direction
direction. It is now obvious that a wave along an arbitrary direction
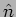 can also be represented by eq. (6.13) if we change
the wave vector to
can also be represented by eq. (6.13) if we change
the wave vector to
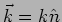 . The wave vector
. The wave vector 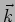 carries
information about both the wavelength
carries
information about both the wavelength 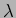 and the direction of
propagation
and the direction of
propagation 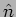 .
.
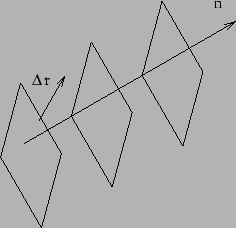
For such a wave, at a fixed instant of time, the phase
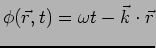 changes only along . The wave fronts are
surfaces perpendicular to
changes only along . The wave fronts are
surfaces perpendicular to 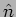 as shown in Figure 6.6.
as shown in Figure 6.6.
Problem: Show the above fact, that is the surface swapped by a
constant
phase at a fixed instant is a two dimensional plane and the wave vector 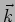 is
normal to that plane.
is
normal to that plane.
The phase difference between two point (shown in Figure 6.6)
separated by
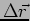 is
is
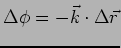 .
.
Figure 6.6:
 |
Problems
- What are the wave number and angular frequency of the wave
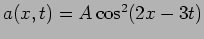 where
where  and
and  are in
are in 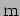 and
and 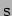 respectively? (
respectively? (
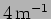 ,
,
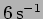 )
)
- What is the wavelength correspnding to the wave vector
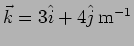 ? (
? (
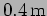 )
)
- A wave with
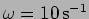 and
and
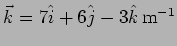 has phase at the
point
has phase at the
point 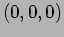 at
at 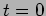 .
[a.] At what time will this value of phase reach the point
.
[a.] At what time will this value of phase reach the point
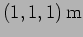 ? [b.] What is the phase at the point
? [b.] What is the phase at the point
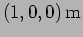 at
at
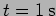 ? [c.] What is the phase velocity of the wave? ([a.]
? [c.] What is the phase velocity of the wave? ([a.]
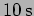 [b.]
[b.]
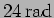 [c.]
[c.]
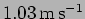
- For a wave with
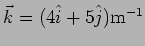 and
and
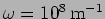 , what are the values of the following?
[a.] wavelength, [b.] frequency
[c.] phase velocity, [d.] phase difference between the two points
, what are the values of the following?
[a.] wavelength, [b.] frequency
[c.] phase velocity, [d.] phase difference between the two points
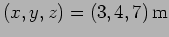 and
and
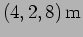 .
.
- The phase of a plane wave is the same at the points
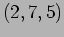 ,
,
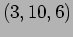 and
and 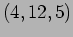 . and the phase is
. and the phase is 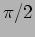 ahead
at
ahead
at 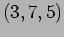 . Determine the wave vector for the wave.[All coordinates
are in
. Determine the wave vector for the wave.[All coordinates
are in  .]
.]
- Two waves of the same frequency have wave vectors
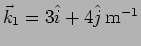 and
and
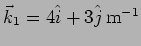 respectively. The two waves have the
same phase at the point
respectively. The two waves have the
same phase at the point
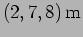 , what is the phase difference
between the waves at the point
, what is the phase difference
between the waves at the point
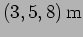 ? (
? (
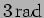 )
)




Next: Electromagnetic Waves.
Up: Sinusoidal Waves.
Previous: Waves in three dimensions.
Contents
Physics 1st Year
2009-01-06
![]() changes only along . The wave fronts are
surfaces perpendicular to
changes only along . The wave fronts are
surfaces perpendicular to ![]() as shown in Figure 6.6.
as shown in Figure 6.6.
![]() is
normal to that plane.
is
normal to that plane.
![]() is
is
![]() .
.