



Next: Waves in an arbitrary
Up: Sinusoidal Waves.
Previous: Phase velocity.
Contents
We have till now considered waves which depend on only one position
coordinate  and time
and time 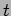 . This is quite adequate when considering
waves on a string as the position along a string can be described by
a single coordinate. It is necessary to bring three spatial
coordinates into the picture when considering a wave
propagating in three dimensional space. A sound wave propagating in
air is an example.
. This is quite adequate when considering
waves on a string as the position along a string can be described by
a single coordinate. It is necessary to bring three spatial
coordinates into the picture when considering a wave
propagating in three dimensional space. A sound wave propagating in
air is an example.
We use the vector
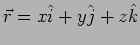 to denote a point in three
dimensional space. The solution which we have been discussing
to denote a point in three
dimensional space. The solution which we have been discussing
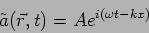 |
(6.12) |
can be interpreted in the context of a three dimensional space. Note
that
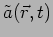 varies only along the direction and not along
varies only along the direction and not along 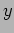 and
and 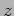 . Considering the phase
. Considering the phase
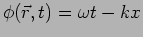 we see that at any
particular instant of time
we see that at any
particular instant of time 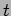 , there are surfaces on which the phase
is constant. The constant phase surfaces of a wave are called wave
fronts. In this case the wave fronts are parallel to the
, there are surfaces on which the phase
is constant. The constant phase surfaces of a wave are called wave
fronts. In this case the wave fronts are parallel to the 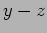 plane
as
shown in Figure 6.5. The wave fronts move along the
plane
as
shown in Figure 6.5. The wave fronts move along the 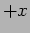 direction
with speed
direction
with speed 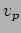 as time evolves. You can check this by following the
motion of the
as time evolves. You can check this by following the
motion of the 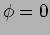 surface shown in Figure 6.5.
surface shown in Figure 6.5.
Figure 6.5:
 |




Next: Waves in an arbitrary
Up: Sinusoidal Waves.
Previous: Phase velocity.
Contents
Physics 1st Year
2009-01-06
![]() to denote a point in three
dimensional space. The solution which we have been discussing
to denote a point in three
dimensional space. The solution which we have been discussing