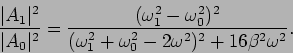Next: Sinusoidal Waves.
Up: Coupled Oscillators
Previous: Normal modes
Contents
As an example we consider a situation where
the two particles are initially at rest in the equilibrium
position. The particle 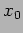 is
given a small displacement
is
given a small displacement 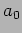 and then left to oscillate.
Using this to determine
and then left to oscillate.
Using this to determine 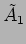 and
and 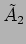 , we finally have
, we finally have
![\begin{displaymath}
x_0 (t) = \frac{a_0}{2} \left[ \cos \ \omega_0 t + \cos \ \omega_1 t
\right]
\end{displaymath}](img404.png) |
(5.13) |
and
![\begin{displaymath}
x_1 (t) = \frac{a_0}{2} \left[ \cos \ \omega_0 t - \cos \ \omega_1 t
\right]
\end{displaymath}](img405.png) |
(5.14) |
The solution can also be written as
![\begin{displaymath}
x_0(t) = a_0 \ \cos \left[\left( \frac{\omega_1 - \omega_0 ...
...ft[ \left( \frac{\omega_0 + \omega_1}{2}
\right) t \right]
\end{displaymath}](img406.png) |
(5.15) |
![\begin{displaymath}
x_1(t) = a_0 \ \sin \left[ \left( \frac{\omega_1 - \omega_0...
...ft[ \left( \frac{\omega_0 + \omega_1}{2}
\right) t \right]
\end{displaymath}](img407.png) |
(5.16) |
It is interesting to consider 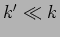 where
the two oscillators are weakly coupled. In this limit
where
the two oscillators are weakly coupled. In this limit
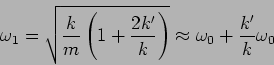 |
(5.17) |
and we have solutions
![\begin{displaymath}
x_0 (t) = \left[ a_0 \ \cos \left(\ \frac{k'}{2 k} \omega_0 t \right)
\ \right] \cos \ \omega_0 t
\end{displaymath}](img410.png) |
(5.18) |
and
![\begin{displaymath}
x_1 (t) = \left[ a_0 \ \sin \left(\ \frac{k'}{2 k} \omega_0 t \right)
\ \right] \sin \ \omega_0 t \,.
\end{displaymath}](img411.png) |
(5.19) |
Figure 5.5:
This shows the motion of 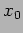 and
and 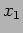 .
.
|
The solution is shown in Figure 5.5. We can think of the
motion as an oscillation with 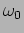 where the amplitude
undergoes a slow modulation at angular frequency
where the amplitude
undergoes a slow modulation at angular frequency
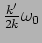 . The oscillations of the two particles are out of phase and
are slowly transferred from the particle which
receives the initial displacement to the particle originally at
rest, and then back again.
. The oscillations of the two particles are out of phase and
are slowly transferred from the particle which
receives the initial displacement to the particle originally at
rest, and then back again.
Problems
- For the coupled oscillator shown in FIgure 5.1
with
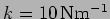 ,
,
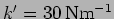 and
and
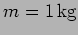 , both particles are
initially at
rest. The system is set into oscillations by displacing
, both particles are
initially at
rest. The system is set into oscillations by displacing
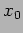 by
by
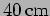 while
while 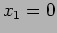 .
.
[a.] What is the angular frequency of the faster normal mode?
[b.] Calculate the average kinetic energy of 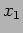 ? [c.] How does the
average kinetic energy of
? [c.] How does the
average kinetic energy of 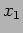 change if the mass of both the
particles is doubled? ([a.]
change if the mass of both the
particles is doubled? ([a.]
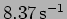 [b.]
[b.]
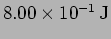 [c.] No change)
[c.] No change)
- For a coupled oscillator
with
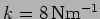 ,
,
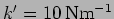 and
, both particles are initially at
rest. The system is set into oscillations by displacing
and
, both particles are initially at
rest. The system is set into oscillations by displacing
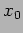 by
by
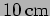 while .
while .
[a.] What are the angular frequencies of the two normal modes of this
system? [b.] With what time period does the instantaneous potential
energy of the middle spring oscillate? [c.] What is the average
potential energy of the middle spring?
- Consider a coupled oscillator
with
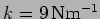 ,
,
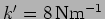 and
and
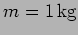 . Initially both particles
have zero velocity with
. Initially both particles
have zero velocity with
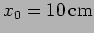 and
and 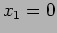 .
[a.] After how much time does the system return to the initial
configuration? [b.] After how much time is the separation between
the two masses maximum? [c.] What are the avergae kinetic and
potential energy?
([a.]
.
[a.] After how much time does the system return to the initial
configuration? [b.] After how much time is the separation between
the two masses maximum? [c.] What are the avergae kinetic and
potential energy?
([a.]
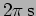 , [b.]
, [b.]
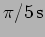 [c.]
[c.]
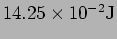 )
)
- A coupled oscillator has
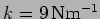 ,
,
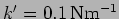 and
and
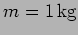 . Initially both particles
have zero velocity with
. Initially both particles
have zero velocity with
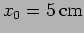 and
and 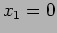 .
After how many oscillations in
.
After how many oscillations in 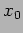 does it completely
die down? (45)
does it completely
die down? (45)
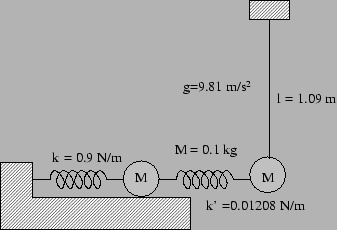
- Find out the frequencies of the normal modes for the
following coupled pendula (see figure 5.6) for small
oscillations.
Calculate time period for beats.
Figure 5.6:
Problem 5 and 6
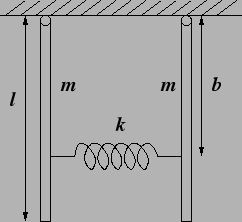 |
- A coupled system is in a vertical plane. Each rod
is of mass
 and length
and length 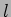 and can freely oscillate about the point of
suspension. The spring is attached at a length
and can freely oscillate about the point of
suspension. The spring is attached at a length 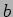 from the points of suspensions
(see figure 5.6). Find the frequencies of normal(eigen) modes. Find
out the ratios of amplitudes of the two oscillators for exciting the
normal(eigen) modes.
from the points of suspensions
(see figure 5.6). Find the frequencies of normal(eigen) modes. Find
out the ratios of amplitudes of the two oscillators for exciting the
normal(eigen) modes.
- Mechanical filter:Damped-forced-coupled oscillator- Suppose one
of the masses in the
system (say mass 1) is under sinusoidal forcing
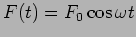 . Include also resistance in the system such that the damping
term is equal to
. Include also resistance in the system such that the damping
term is equal to
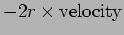 .
Write down the equations of motion for the above system.
.
Write down the equations of motion for the above system.
Solution 7:
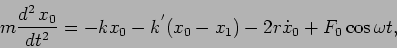 |
(5.20) |
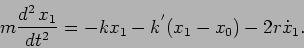 |
(5.21) |
Rearranging the terms we have (with notations of forced oscillations),
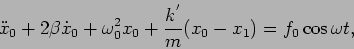 |
(5.22) |
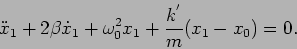 |
(5.23) |
- Solve the equations by identifying the normal modes.
Solution 8: Decouple the equations using 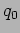 and
and 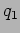 .
.
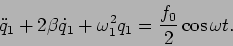 |
(5.25) |
- Write down the solutions of
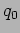 and
and 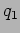 as
as
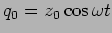 and
and
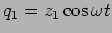 respectively,
with
respectively,
with
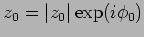 and
and
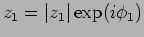 .
Find
.
Find
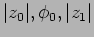 and
and 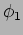 .
.
- Find amplitudes of the original masses, viz
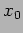 and
and
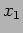 .
.
Do phasor addition and subtraction to evaluate amplitudes 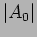 and
and
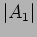 . Find also the the phases
. Find also the the phases 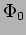 and
and 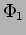 .
.
- Using above results show that:
- Plot the above ratio of amplitudes of two coupled
oscillators as a function of forcing frequency
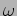 using very
small damping (i.e. neglecting the
using very
small damping (i.e. neglecting the 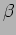 term). From there
observe that the ratio of amplitudes dies as the forcing frequency
goes below
term). From there
observe that the ratio of amplitudes dies as the forcing frequency
goes below 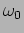 or above
or above 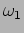 . So the system works as a
band pass filter, i.e. the unforced mass has large amplitude only when
the forcing frequency is in between
. So the system works as a
band pass filter, i.e. the unforced mass has large amplitude only when
the forcing frequency is in between 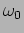 and
and
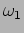 . Otherwise it does not respond to forcing.
. Otherwise it does not respond to forcing.




Next: Sinusoidal Waves.
Up: Coupled Oscillators
Previous: Normal modes
Contents
Physics 1st Year
2009-01-06
![]() where
the two oscillators are weakly coupled. In this limit
where
the two oscillators are weakly coupled. In this limit
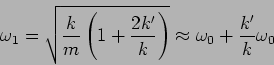
![\begin{displaymath}
x_0 (t) = \left[ a_0 \ \cos \left(\ \frac{k'}{2 k} \omega_0 t \right)
\ \right] \cos \ \omega_0 t
\end{displaymath}](img410.png)
![\begin{displaymath}
x_1 (t) = \left[ a_0 \ \sin \left(\ \frac{k'}{2 k} \omega_0 t \right)
\ \right] \sin \ \omega_0 t \,.
\end{displaymath}](img411.png)
![]() where the amplitude
undergoes a slow modulation at angular frequency
where the amplitude
undergoes a slow modulation at angular frequency
![]() . The oscillations of the two particles are out of phase and
are slowly transferred from the particle which
receives the initial displacement to the particle originally at
rest, and then back again.
. The oscillations of the two particles are out of phase and
are slowly transferred from the particle which
receives the initial displacement to the particle originally at
rest, and then back again.
![]() ? [c.] How does the
average kinetic energy of
? [c.] How does the
average kinetic energy of ![]() change if the mass of both the
particles is doubled? ([a.]
change if the mass of both the
particles is doubled? ([a.]
![]() [b.]
[b.]
![]() [c.] No change)
[c.] No change)
![]() and
and ![]() .
.