



Next: Normal modes
Up: lect_notes
Previous: The Raman Effect
Contents
Consider two idential simple harmonic oscillators of mass  and
spring constant
and
spring constant 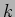 as shown in Figure 5.1 (a.). The two
oscillators are independent with
as shown in Figure 5.1 (a.). The two
oscillators are independent with
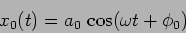 |
(5.1) |
and
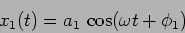 |
(5.2) |
where they both oscillate with the same frequency
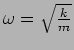 . The amplitudes
. The amplitudes 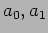 and the
phases
and the
phases 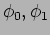 of the two oscillators are in no way
interdependent. The question which we take up for discussion here is
what happens if the two masses are coupled by a third spring as shown
in Figure 1 (b.).
of the two oscillators are in no way
interdependent. The question which we take up for discussion here is
what happens if the two masses are coupled by a third spring as shown
in Figure 1 (b.).
Figure 5.1:
This shows two identical spring-mass systems. In (a.) the two
oscillators are independent whereas in (b.) they are coupled through
an extra spring.
![\includegraphics[angle=0 width=0.8\textwidth]{chapt5//fig1.eps}](img381.png) |
The motion of the two oscillators is now coupled through the third
spring of spring constant 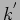 . It is clear that the oscillation of
one oscillator affects the second. The phases and amplitudes of the
two oscillators are no longer independent and the frequency of
oscillation is also modified. We proceed to calculate these effects
below.
. It is clear that the oscillation of
one oscillator affects the second. The phases and amplitudes of the
two oscillators are no longer independent and the frequency of
oscillation is also modified. We proceed to calculate these effects
below.
The equations governing the coupled oscillators are
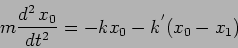 |
(5.3) |
and
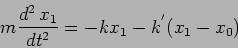 |
(5.4) |
Subsections




Next: Normal modes
Up: lect_notes
Previous: The Raman Effect
Contents
Physics 1st Year
2009-01-06
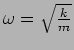 . The amplitudes
. The amplitudes ![]() . It is clear that the oscillation of
one oscillator affects the second. The phases and amplitudes of the
two oscillators are no longer independent and the frequency of
oscillation is also modified. We proceed to calculate these effects
below.
. It is clear that the oscillation of
one oscillator affects the second. The phases and amplitudes of the
two oscillators are no longer independent and the frequency of
oscillation is also modified. We proceed to calculate these effects
below.