



Next: Resonance
Up: Coupled Oscillators
Previous: Coupled Oscillators
Contents
The technique to solve such coupled differential equations is to
identify linear combinations of 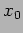 and
and 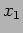 for which the
equations become decoupled. In this case it is very easy to
identify such variables
for which the
equations become decoupled. In this case it is very easy to
identify such variables
These are referred to as as the normal modes (or eigen modes)
of the system and
the equations governing them are
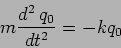 |
(5.6) |
and
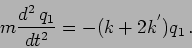 |
(5.7) |
The two normal modes execute simple harmonic oscillations with
respective angular frequencies
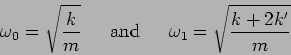 |
(5.8) |
In this case the normal modes lend themselves to a simple
physical interpretation where.
The normal mode 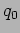 represents the center of mass. The center of
mass behaves as if it were a particle of mass
represents the center of mass. The center of
mass behaves as if it were a particle of mass 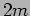 attached to two
springs (Figure 5.2) and its oscillation frequency is the same
as that of the individual decoupled oscillators
attached to two
springs (Figure 5.2) and its oscillation frequency is the same
as that of the individual decoupled oscillators
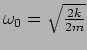 .
.
Figure 5.2:
This shows the spring mass equivalent of the normal mode
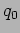 which corresponds to the center of mass.
which corresponds to the center of mass.
|
The normal mode 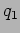 represents the relative motion of he two masses
which leaves the center of mass unchanged. This can be thought of as
the motion of two particles of mass
represents the relative motion of he two masses
which leaves the center of mass unchanged. This can be thought of as
the motion of two particles of mass  connected to a spring of
spring constant
connected to a spring of
spring constant
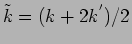 as shown in Figure
5.3. The oscillation frequency of this normal mode
as shown in Figure
5.3. The oscillation frequency of this normal mode
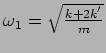 is always higher than that of
the individual uncoupled oscillators (or the center of mass).
The modes
is always higher than that of
the individual uncoupled oscillators (or the center of mass).
The modes 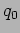 and
and 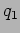 are often referred to as the slow mode
and the fast mode respectively.
are often referred to as the slow mode
and the fast mode respectively.
Figure 5.3:
This shows the spring mass equivalent of the normal mode
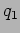 which corresponds to two particles connected through a spring.
which corresponds to two particles connected through a spring.
|
We may interpret 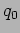 as a mode of oscillation where
the two masses oscillate with exactly the same phase, and
as a mode of oscillation where
the two masses oscillate with exactly the same phase, and 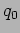 as a
mode where they have a phase difference of
as a
mode where they have a phase difference of 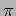 (Figure
5.4). Recollect that the
phases of the two masses are independent when the two masses are
not coupled. Introducing a coupling causes the phases to
be interdependent.
(Figure
5.4). Recollect that the
phases of the two masses are independent when the two masses are
not coupled. Introducing a coupling causes the phases to
be interdependent.
Figure 5.4:
This shows the motion corresponding to the two normal
modes 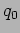 and
and 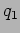 respectively.
respectively.
|
The normal modes have solutions
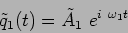 |
(5.10) |
where it should be bourne in mind that 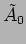 and
and 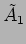 are complex numbers with both amplitude and phase ie.
are complex numbers with both amplitude and phase ie.
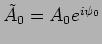 etc. We then have the solutions
etc. We then have the solutions
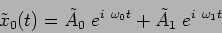 |
(5.11) |
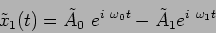 |
(5.12) |
The complex amplitudes 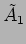 and
and 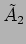 have to be determined from
the initial conditions, four initial conditions are required in
total.
have to be determined from
the initial conditions, four initial conditions are required in
total.




Next: Resonance
Up: Coupled Oscillators
Previous: Coupled Oscillators
Contents
Physics 1st Year
2009-01-06
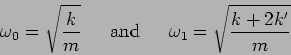
![]() represents the center of mass. The center of
mass behaves as if it were a particle of mass
represents the center of mass. The center of
mass behaves as if it were a particle of mass ![]() attached to two
springs (Figure 5.2) and its oscillation frequency is the same
as that of the individual decoupled oscillators
attached to two
springs (Figure 5.2) and its oscillation frequency is the same
as that of the individual decoupled oscillators
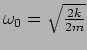 .
.
![]() represents the relative motion of he two masses
which leaves the center of mass unchanged. This can be thought of as
the motion of two particles of mass
represents the relative motion of he two masses
which leaves the center of mass unchanged. This can be thought of as
the motion of two particles of mass ![]() connected to a spring of
spring constant
connected to a spring of
spring constant
![]() as shown in Figure
5.3. The oscillation frequency of this normal mode
as shown in Figure
5.3. The oscillation frequency of this normal mode
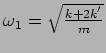 is always higher than that of
the individual uncoupled oscillators (or the center of mass).
The modes
is always higher than that of
the individual uncoupled oscillators (or the center of mass).
The modes ![]() and
and ![]() are often referred to as the slow mode
and the fast mode respectively.
are often referred to as the slow mode
and the fast mode respectively.
![]() as a mode of oscillation where
the two masses oscillate with exactly the same phase, and
as a mode of oscillation where
the two masses oscillate with exactly the same phase, and ![]() as a
mode where they have a phase difference of
as a
mode where they have a phase difference of ![]() (Figure
5.4). Recollect that the
phases of the two masses are independent when the two masses are
not coupled. Introducing a coupling causes the phases to
be interdependent.
(Figure
5.4). Recollect that the
phases of the two masses are independent when the two masses are
not coupled. Introducing a coupling causes the phases to
be interdependent.