



Next: Quantum Mechanics
Up: lect_notes
Previous: Probability amplitude
Contents
Consider a process whose outcome is uncertain. For example, we
throw a dice. The value the dice returns can have 6 values,
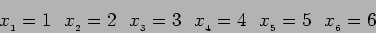 |
(19.1) |
We can ask the question ``What is the probability of getting an
outcome 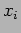 when you throw the dice?'' This probability can be
calculated using,
when you throw the dice?'' This probability can be
calculated using,
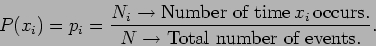 |
(19.2) |
For a fair dice
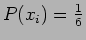 for all the six possible
outcomes as shown in Figure 19.1.
for all the six possible
outcomes as shown in Figure 19.1.
Figure 19.1:
Probabilities of different outcomes for a fair dice
|
|
What is the expected outcome when we throw the dice? We next
calculate the expectation value which again is an integral,
Suppose we have a biased dice which produces only 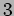 and
and 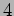 . We have
. We have
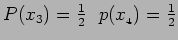 , the rest are all
zero as shown in Figure 19.2.
, the rest are all
zero as shown in Figure 19.2.
Figure 19.2:
Probabilities of different outcomes for a biased dice
|
|
Calculating the expectation value for the biased dice we have
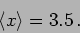 |
(19.4) |
The expectation value is unchanged even though the probability
distributions are different. Whether we throw the unbiased dice
or the biased dice, the expected value is the same. Each time we
throw the dice, we will get a different value . In both cases the
values will be spread around 3.5 . The values will have a larger
spread for the fair dice as compared to the biased one. How to
characterize this? The root mean square or standard deviation
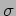 tells this. The variance
tells this. The variance 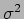 is calculated as,
is calculated as,
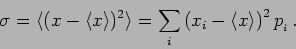 |
(19.5) |
Larger the value of 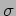 the more is the spread. Let us
calculate the variance for the fair dice,
the more is the spread. Let us
calculate the variance for the fair dice,
![\begin{displaymath}
\sigma^2=\frac{1}{6} \left[ (1-3.5)^2+(2-3.5)^2+ ... + (6-3.5)^2
\right],
\end{displaymath}](img1501.png) |
(19.6) |
which gives the standard deviation 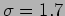 . For the biased dice
we have
. For the biased dice
we have
![\begin{displaymath}
\sigma^2=\frac{1}{2} \left[ (3-3.5)^2+(4-3.5)^2
\right],
\end{displaymath}](img1503.png) |
(19.7) |
which gives 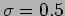 . We see that
the fair dice has a larger variance and standard deviation then the
unbiased one. The uncertainty in the outcome is larger for the fair
dice and is smaller for the biased one.
. We see that
the fair dice has a larger variance and standard deviation then the
unbiased one. The uncertainty in the outcome is larger for the fair
dice and is smaller for the biased one.
We now shift over attention to continuous variables. For example, x is
a random variable which can have any value between 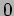 and
and 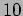 (Figure 19.3). What is
the probability that x has a value
(Figure 19.3). What is
the probability that x has a value 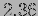 ?
?
This probability is zero. We see this as follows. The probability
of any value between 0 and 10 is the same. There are infinite
points between 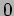 and
and 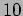 and the probability of getting exactly
and the probability of getting exactly
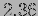 is,
is,
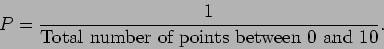 |
(19.8) |
The denominator is infinitely
large and the probability is thus zero. A correct question would
be, what is the probability that  has a value between
and
has a value between
and 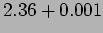 . We can calculate this as,
. We can calculate this as,
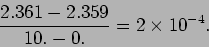 |
(19.9) |
For a continuous variable it does not make sense to ask for the
probability of its having a particular value  . A meaningful
question is, what is the probability that it has a value in the
interval
. A meaningful
question is, what is the probability that it has a value in the
interval 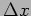 around the value
around the value  .
.
Making 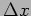 an infinitesimal we have,
an infinitesimal we have,
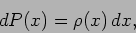 |
(19.10) |
where 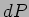 is probability of getting a value in the internal
is probability of getting a value in the internal
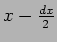 to
to
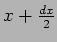 . If all values in the range
. If all values in the range
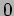 to
to 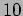 are equally probable then,
are equally probable then,
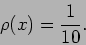 |
(19.11) |
The function 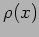 is called the probability density. It has the
properties:
is called the probability density. It has the
properties:
- It is necessarily positive
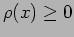
-
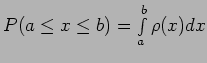 gives the
probability that
gives the
probability that  has a value in the range
has a value in the range 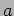 to
to 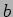 .
.
-
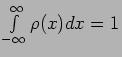 Total
probability is
Total
probability is
Let us consider an example (Figure 19.4) where
We first normalize the probability density. This means
to ensure that
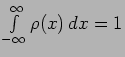 .
Applying this condition we have,
.
Applying this condition we have,
which gives us,
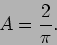 |
(19.14) |
We next calculate the expectation value
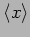 . The
sum in equation (19.3) is now replaced by an integral and,
. The
sum in equation (19.3) is now replaced by an integral and,
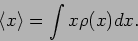 |
(19.15) |
Evaluating this we have,
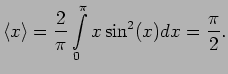 |
|
|
(19.16) |
We next calculate the variance,
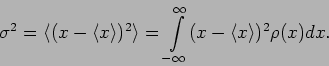 |
(19.17) |
This can be simplified as,
Problem Calculate the variance 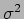 for the
probability distribution in equation (19.12).
for the
probability distribution in equation (19.12).
We now return to the wave 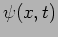 associated with every
particle. The laws governing this wave are referred to as Quantum
Mechanics. We have already learnt that this wave is to be
interpreted as the probability amplitude. The probability
amplitude can be used to calculate the probability density
associated with every
particle. The laws governing this wave are referred to as Quantum
Mechanics. We have already learnt that this wave is to be
interpreted as the probability amplitude. The probability
amplitude can be used to calculate the probability density
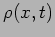 using,
using,
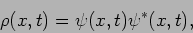 |
(19.19) |
and
gives the probability of finding the particle
in an interval 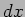 around the point
around the point  . The expectation value of
the particle's position can be calculated using,
. The expectation value of
the particle's position can be calculated using,
This is the expected
value if we measure the particle's position. Typically, a
measurement will not yield this value. If the position of many
identical particles all of which have the ``wave function''
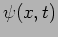 are measured these values will be centered around
are measured these values will be centered around
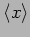 . The spread in the measured values of
. The spread in the measured values of  is
quantified through the variance,
is
quantified through the variance,
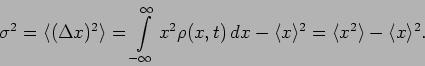 |
(19.20) |
The standard deviation which is also denoted as
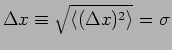 gives an estimate of the
uncertainty in the particle's position.
gives an estimate of the
uncertainty in the particle's position.
Problems
- The measurement of a particle's position
 in seven identical
replicas of the same system we get values
in seven identical
replicas of the same system we get values 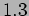 ,
, 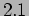 , ,
, ,
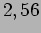 ,
, 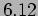 ,
, 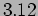 and
and 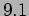 . What are the expectation value and
uncertainty in
. What are the expectation value and
uncertainty in  ?
?
- In an experiment the value of
 is found to be different each
time the experiment is performed. The values of
is found to be different each
time the experiment is performed. The values of  are found to be
always positive, and the distribution is found to be well described
by a probability density
are found to be
always positive, and the distribution is found to be well described
by a probability density
- a.
- What is the expected value of
 if the experiment is
performed once?
if the experiment is
performed once?
- b.
- What is the uncertainty
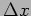 ?
?
- c.
- What is the probability that
 is less than
is less than
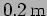 ?
?
- d.
- The experiment is performed ten times. What is the
probability
that all the values of
 are less than
are less than
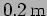 ?
?
- For a Gaussian probability density distribution
- a.
- Calculate the normalization coefficient
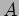 .
.
- b.
- What is the expectation value
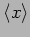 ?
?
- c.
- What is the uncertainty
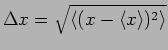 ?
?
- d.
- What is the probability that
 has a positive value?
has a positive value?




Next: Quantum Mechanics
Up: lect_notes
Previous: Probability amplitude
Contents
Physics 1st Year
2009-01-06
![]() for all the six possible
outcomes as shown in Figure 19.1.
for all the six possible
outcomes as shown in Figure 19.1.
![]() tells this. The variance
tells this. The variance ![]() is calculated as,
is calculated as,
![]() and
and ![]() (Figure 19.3). What is
the probability that x has a value
(Figure 19.3). What is
the probability that x has a value ![]() ?
?
![]() and
and ![]() and the probability of getting exactly
and the probability of getting exactly
![]() is,
is,
![]() has a value between
and
has a value between
and ![]() . We can calculate this as,
. We can calculate this as,
![]() an infinitesimal we have,
an infinitesimal we have,
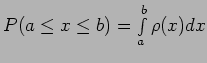 gives the
probability that
gives the
probability that 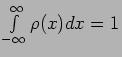 Total
probability is
Total
probability is
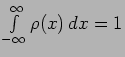 .
Applying this condition we have,
.
Applying this condition we have,
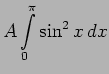
![$\displaystyle \left. \frac{A}{2} \left[ \pi - \frac{1}{2} \sin (2x)\right\vert _0^\pi
\right] = \frac{\pi A}{2} =1,$](img1527.png)
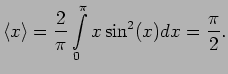
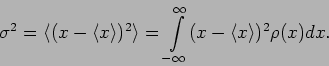
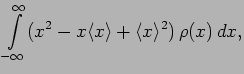
![]() for the
probability distribution in equation (19.12).
for the
probability distribution in equation (19.12).
![]() associated with every
particle. The laws governing this wave are referred to as Quantum
Mechanics. We have already learnt that this wave is to be
interpreted as the probability amplitude. The probability
amplitude can be used to calculate the probability density
associated with every
particle. The laws governing this wave are referred to as Quantum
Mechanics. We have already learnt that this wave is to be
interpreted as the probability amplitude. The probability
amplitude can be used to calculate the probability density
![]() using,
using,
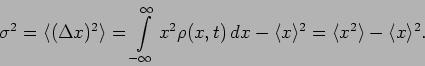
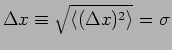 gives an estimate of the
uncertainty in the particle's position.
gives an estimate of the
uncertainty in the particle's position.
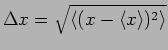 ?
?