



Next: Solving the wave equation
Up: The wave equation.
Previous: Longitudinal elastic waves
Contents
In this section we discuss the transverse vibrations in stretched
strings. We consider a uniform stretched string having a tension
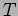 . We take a particular section of this string which is
disturbed from its mean position as shown in the figure
15.5 below. The displacement of the point
. We take a particular section of this string which is
disturbed from its mean position as shown in the figure
15.5 below. The displacement of the point  on the
string at time
on the
string at time 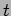 is denoted with
is denoted with 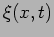 . Further we assume
that the disturbances are small and strictly orthogonal to the
undisturbed string.
. Further we assume
that the disturbances are small and strictly orthogonal to the
undisturbed string.
Figure 15.5:
A particular section of the string
|
|
The horizontal component of the force is,
where 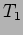 and
and 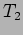 are the new tensions at points
are the new tensions at points  and
and
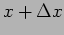 respectively. Hence,
respectively. Hence,
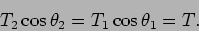 |
(15.20) |
Now coming to the vertical component of the force, we have,
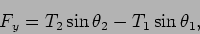 |
(15.21) |
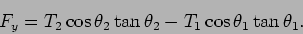 |
(15.22) |
Using the equation (15.20), we obtain,
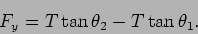 |
(15.23) |
Now 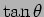 at a particular point is nothing but the slope at
that point of the disturbed string, so we can write,
at a particular point is nothing but the slope at
that point of the disturbed string, so we can write,
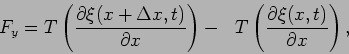 |
(15.24) |
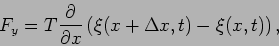 |
(15.25) |
The above force would produce the vertical acceleration in that
particular section of the string. Hence,
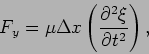 |
(15.27) |
where 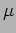 is the mass per unit length of the string. Now from
equations (15.26) and (15.27) we have,
is the mass per unit length of the string. Now from
equations (15.26) and (15.27) we have,
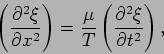 |
(15.28) |
which can be again written as equation (15.13), that is,
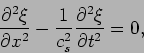 |
(15.29) |
where now the phase velocity, 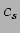 , of the wave is equal to
, of the wave is equal to
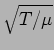 .
.




Next: Solving the wave equation
Up: The wave equation.
Previous: Longitudinal elastic waves
Contents
Physics 1st Year
2009-01-06
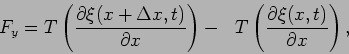
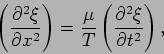
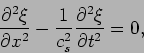
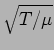 .
.