



Next: The wave equation.
Up: lect_notes
Previous: X-ray Diffraction
Contents
In this chapter we consider the superposition of two waves of
different frequencies. At a fixed point along the propagation
direction of the waves, the time evolution of the two wave are,
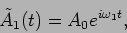 |
(14.1) |
and
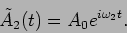 |
(14.2) |
The superposition of these two waves of equal amplitude is
which can be written as,
where
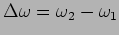 and
and
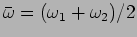 are respectively the difference
and the average of the two frequencies. If the two frequencies
are respectively the difference
and the average of the two frequencies. If the two frequencies
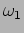 and
and 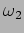 are very close, and the difference in
frequencies
are very close, and the difference in
frequencies 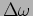 is much smaller than
is much smaller than 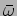 , we
can think of the resultant as a fast varying wave with frequency
, we
can think of the resultant as a fast varying wave with frequency
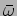 whose amplitude varies slowly at a frequency
whose amplitude varies slowly at a frequency
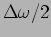 . The intensity of the resulting wave is modulated at a
frequency
. The intensity of the resulting wave is modulated at a
frequency
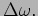 This slow modulation of the intensity
is referred to as beats. This modulation is heard when two strings
of a musical instrument are nearly tuned and this is useful in
tuning musical instruments.
This slow modulation of the intensity
is referred to as beats. This modulation is heard when two strings
of a musical instrument are nearly tuned and this is useful in
tuning musical instruments.
In the situation where the two amplitudes are different we have,
Again we see that we have a fast varying component whose amplitude
is modulated slowly . The intensity of the resultant wave is,
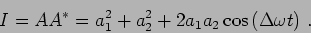 |
(14.6) |
We see that the intensity oscillates at the frequency difference
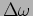 , and it
never goes to zero if the two amplitudes are different.
, and it
never goes to zero if the two amplitudes are different.
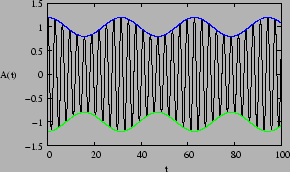
Figure 14.1:
A modulated
wave
 |
Radio transmission based on ``amplitude modulation'' is the opposite
of this. The transmitter has a generator which produces a sinusoidal
electrical wave at a high frequency, say
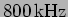 which is
the transmission frequency. This is called the carrier wave. The
signal which is to be transmitted, say sound, is a relatively slowly
varying signal in the frequency range
which is
the transmission frequency. This is called the carrier wave. The
signal which is to be transmitted, say sound, is a relatively slowly
varying signal in the frequency range
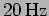 to
to
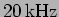 .
The sound is converted to an electrical signal and the amplitude of
the carrier wave is modulated by the slowly varying
signal. Mathematically,
.
The sound is converted to an electrical signal and the amplitude of
the carrier wave is modulated by the slowly varying
signal. Mathematically,
![\begin{displaymath}
\tilde A(t) = \left[ 1+ f(t) \right] e^{i \omega_c t },
\end{displaymath}](img1108.png) |
(14.7) |
where 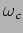 is the angular frequency of the carrier wave, and
is the angular frequency of the carrier wave, and
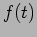 is the slowly varying signal. As an example we consider a
situation where the signal has a single frequency component,
is the slowly varying signal. As an example we consider a
situation where the signal has a single frequency component,
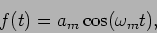 |
(14.8) |
where 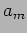 is the amplitude and
is the amplitude and 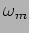 the frequency of the
modulating signal. The transmitted signal
the frequency of the
modulating signal. The transmitted signal 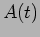 is shown in
Figure 14.1. The envelope contains the signal. This can
be recovered at the receiver by discarding the carrier and
retaining only the envelope. The transmitted signal can be
expressed as,
is shown in
Figure 14.1. The envelope contains the signal. This can
be recovered at the receiver by discarding the carrier and
retaining only the envelope. The transmitted signal can be
expressed as,
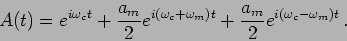 |
(14.9) |
We see that though the transmitter originally produces output only
at a single frequency 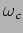 when there is no modulation, it
starts transmitting two other frequencies
when there is no modulation, it
starts transmitting two other frequencies
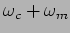 and
and
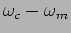 once the signal is modulated. These new
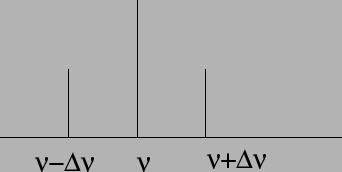
frequencies are referred to as sidebands. If we plot the spectrum
of the radiation from the transmitter, we see that the energy is
distributed in three frequencies as shown in
Figure 14.2.
once the signal is modulated. These new
frequencies are referred to as sidebands. If we plot the spectrum
of the radiation from the transmitter, we see that the energy is
distributed in three frequencies as shown in
Figure 14.2.
Figure 14.2:
Sidebands
 |
For a more complicated sound signal, the sidebands will be spread
over a range of frequencies instead of a few discrete frequencies.
The audible frequency range extends upto
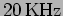 but the
transmitters and receivers usually do not work beyond
but the
transmitters and receivers usually do not work beyond
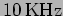 . So a radio station transmitting at
. So a radio station transmitting at
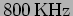 will
actually be transmitting modulated signal in the frequency range
will
actually be transmitting modulated signal in the frequency range
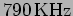 to
to
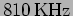 .
.
If our radio
receiver were so sensitive that it picks up only a very small range of
frequency around
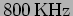 ,
we would not be able to hear the sound
that is being transmitted as the higher frequency components would be
missing.
,
we would not be able to hear the sound
that is being transmitted as the higher frequency components would be
missing.
Further, if there were two stations one at
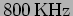 and
another at
and
another at
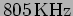 , the transmissions from the two
stations would overlap and we would get a garbage sound from our
receivers. The stations should transmit at frequencies that are
sufficiently apart so that they do not overlap. Typically the
frequency range
to
, the transmissions from the two
stations would overlap and we would get a garbage sound from our
receivers. The stations should transmit at frequencies that are
sufficiently apart so that they do not overlap. Typically the
frequency range
to
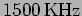 is
available for AM transmission and it is possible to accommodate a
large number of stations.
is
available for AM transmission and it is possible to accommodate a
large number of stations.
We next consider the full position and time dependence of the
superposition of two waves of different frequencies. Assuming
equal amplitudes for the two waves we have,
![\begin{displaymath}
A(t) = A[e^{i (\omega_1t - k_1 x ) } + e^{i (\omega_2 t- k_2 x ) }] \,.
\end{displaymath}](img1126.png) |
(14.10) |
Proceeding in exactly the same way as when we considered only the
time dependence, we now have,
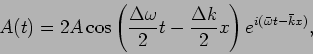 |
(14.11) |
where
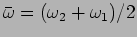 and
and
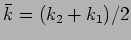 are the mean angular frequency and
wave number respectively, and
are the mean angular frequency and
wave number respectively, and
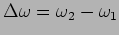 and
and
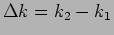 are the difference in the angular frequency and
wave number respectively.
are the difference in the angular frequency and
wave number respectively.
Let us consider a situation where the two frequencies are very
close such that
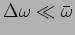 and
and
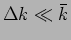 the resultant (equation (14.11)) can then be
interpreted as a travelling wave with angular frequency and wave
number
the resultant (equation (14.11)) can then be
interpreted as a travelling wave with angular frequency and wave
number 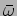 and
and 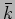 respectively. This wave has a
phase velocity,
respectively. This wave has a
phase velocity,
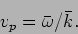 |
(14.12) |
The amplitude of this wave undergoes a slow modulation. The modulation
itself is a travelling wave that propagates at a speed
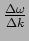 . The speed at which the modulation propagates is
called the group velocity, and we have
. The speed at which the modulation propagates is
called the group velocity, and we have
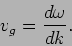 |
(14.13) |
As discussed earlier, it is possible to transmit signals using waves by
modulating the amplitude. Usually (but not always) signals propagate
at the group velocity.
There are situations where the phase velocity is greater than the
speed of light in vacuum, but the group velocity usually comes out
to be smaller . In all cases it is found that no signal propagates
at a speed faster than the speed of light in vacuum. This is one
of the
fundamental assumptions in Einstein's Theory of Relativity.
Problems
- Consider the superposition of two waves with different
angular frequencies
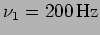 and
and
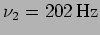 . The two waves are in phase at time
. The two waves are in phase at time 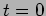 . [a.] After
how much time are the two waves exactly out of phase and when are they
exactly in phase again? [b.] What happens to the intensity of the
superposed wave?
. [a.] After
how much time are the two waves exactly out of phase and when are they
exactly in phase again? [b.] What happens to the intensity of the
superposed wave?
- Consider the superposition of two fast oscillating signals
with
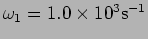 and
and
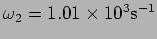 .
The intensity of the
resulting signal
.
The intensity of the
resulting signal 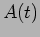 is found to have beats where the intensity
oscillates slowly.
is found to have beats where the intensity
oscillates slowly.
- (
 .)
.)
- What is the time period of the beats?
- (
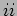 .)
.)
- What is the ratio of the minimum intensity to the maximum
intensity?
- The amplitude of a carrier wave of frequency
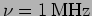 is modulated with the signal
where
is modulated with the signal
where
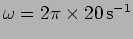 . What are the frequencies
of the different side bands?
. What are the frequencies
of the different side bands?
- The two strings of a guitar which is being tuned are found to
produce beats of time period
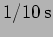 . Also, the minimum
intensity is
. Also, the minimum
intensity is 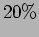 of the maximum intensity. What is the frequency
difference between the two string? What is the ratio of the
vibration amplitudes in the two strings?
of the maximum intensity. What is the frequency
difference between the two string? What is the ratio of the
vibration amplitudes in the two strings?
- The refractive index of x-rays inside materials, is
where a is a constant whose value depends on the properties of the
material. Calculate the phase velocity and the group velocity.
Solution
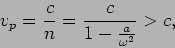 |
(14.15) |
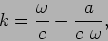 |
(14.16) |
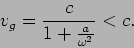 |
(14.17) |
- Consider the superposition of two waves,
with wavelengths
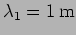 and
and
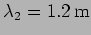 . The wave has a dispersion relation,
. The wave has a dispersion relation,
Treating the wave as a slow modulation on a faster carrier
wave,
- a.
- What are the angular frequency, wave number and phase
velocity of the carrier wave?
- b.
- What are the angular frequency and wave number of the
modulation?
- c.
- At what speed does the modulation propagate?
- The dispersion relation for free relativistic electron
waves is
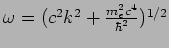 .
Show that the product of phase and group velocity of the wave is a
constant.
.
Show that the product of phase and group velocity of the wave is a
constant.
- A wave packet in a certain medium is represented by the
following
Find group velocity and phase
velocity for the packet. Plot the phase velocity in the medium as a function of wave
number k, near k=1.




Next: The wave equation.
Up: lect_notes
Previous: X-ray Diffraction
Contents
Physics 1st Year
2009-01-06
![]() which is
the transmission frequency. This is called the carrier wave. The
signal which is to be transmitted, say sound, is a relatively slowly
varying signal in the frequency range
which is
the transmission frequency. This is called the carrier wave. The
signal which is to be transmitted, say sound, is a relatively slowly
varying signal in the frequency range
![]() to
to
![]() .
The sound is converted to an electrical signal and the amplitude of
the carrier wave is modulated by the slowly varying
signal. Mathematically,
.
The sound is converted to an electrical signal and the amplitude of
the carrier wave is modulated by the slowly varying
signal. Mathematically,
![]() but the
transmitters and receivers usually do not work beyond
but the
transmitters and receivers usually do not work beyond
![]() . So a radio station transmitting at
. So a radio station transmitting at
![]() will
actually be transmitting modulated signal in the frequency range
will
actually be transmitting modulated signal in the frequency range
![]() to
to
![]() .
.
![]() ,
we would not be able to hear the sound
that is being transmitted as the higher frequency components would be
missing.
,
we would not be able to hear the sound
that is being transmitted as the higher frequency components would be
missing.
![]() and
another at
and
another at
![]() , the transmissions from the two
stations would overlap and we would get a garbage sound from our
receivers. The stations should transmit at frequencies that are
sufficiently apart so that they do not overlap. Typically the
frequency range
to
, the transmissions from the two
stations would overlap and we would get a garbage sound from our
receivers. The stations should transmit at frequencies that are
sufficiently apart so that they do not overlap. Typically the
frequency range
to
![]() is
available for AM transmission and it is possible to accommodate a
large number of stations.
is
available for AM transmission and it is possible to accommodate a
large number of stations.
![]() and
and
![]() the resultant (equation (14.11)) can then be
interpreted as a travelling wave with angular frequency and wave
number
the resultant (equation (14.11)) can then be
interpreted as a travelling wave with angular frequency and wave
number ![]() and
and ![]() respectively. This wave has a
phase velocity,
respectively. This wave has a
phase velocity,
![]() . The speed at which the modulation propagates is
called the group velocity, and we have
. The speed at which the modulation propagates is
called the group velocity, and we have