



Next: Diffraction
Up: Coherence
Previous: Spatial Coherence
Contents
The Michelson interferometer measures the temporal coherence of
the wave. Here a single wave front 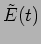 is split into two
is split into two
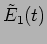 and
and
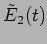 at the beam splitter. This is referred to
as division of amplitude. The two waves are then superposed, one
of the waves being given an extra time delay
at the beam splitter. This is referred to
as division of amplitude. The two waves are then superposed, one
of the waves being given an extra time delay 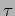 through the
difference in the arm lengths. The intensity of the fringes is
through the
difference in the arm lengths. The intensity of the fringes is
where it is last term involving
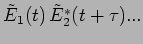 which is responsible for interference.
In our analysis of the Michelson interferometer in the previous chapter
we had assumed that the incident wave is purely monochromatic ie.
which is responsible for interference.
In our analysis of the Michelson interferometer in the previous chapter
we had assumed that the incident wave is purely monochromatic ie.
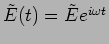 whereby
whereby
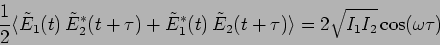 |
(11.10) |
The above assumption is an idealization that we adopt because it
simplifies the analysis. In reality we do not have waves of a single
frequency, there is always a finite spread in frequencies. How does
this affect eq. 11.10?
As an example let us consider two frequencies
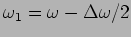 and
and
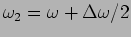 with
with
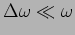
![\begin{displaymath}
\tilde{E}(t)=\tilde{a}\left[ e^{i \omega_1 t} + e^{i \omega_2 t} \right]\,.
\end{displaymath}](img898.png) |
(11.11) |
This can also be written as
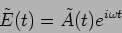 |
(11.12) |
which is a wave of angular frequency 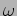 whose amplitude
varies slowly with time.
We now consider a more realistic situation where we have many
frequencies in the range
whose amplitude
varies slowly with time.
We now consider a more realistic situation where we have many
frequencies in the range
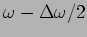 to
to
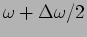 . The resultant will again be of the same
form as eq. (11.12) where there is a wave with angular
frequency
. The resultant will again be of the same
form as eq. (11.12) where there is a wave with angular
frequency 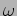 whose
amplitude
whose
amplitude 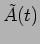 varies slowly on the timescale
varies slowly on the timescale
Figure 11.4:
Variation of E
with time for monochromatic and polychromatic light
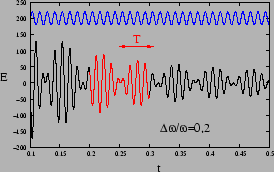 |
Note that the amplitude 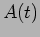 and phase
and phase 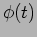 of the complex
amplitude
of the complex
amplitude 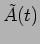 both vary slowly with timescale T.
Figure 11.4 shows a situation where
both vary slowly with timescale T.
Figure 11.4 shows a situation where
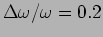 , a pure sinusoidal wave of the same frequency
is shown for comparison. What happens to eq. (11.10) in
the presence of a finite spread in frequencies? It now gets
modified to
, a pure sinusoidal wave of the same frequency
is shown for comparison. What happens to eq. (11.10) in
the presence of a finite spread in frequencies? It now gets
modified to
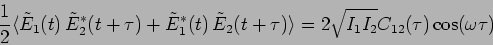 |
(11.13) |
where
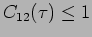 . Here
. Here 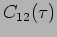 is the temporal
coherence of the two waves
is the temporal
coherence of the two waves
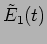 and
and
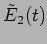 for a time delay
for a time delay
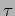 .
Two waves are perfectly coherent if
, partially
coherent if
.
Two waves are perfectly coherent if
, partially
coherent if
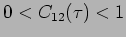 and incoherent if
and incoherent if
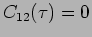 .
Typically the coherence time
.
Typically the coherence time 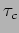 of a wave is decided by the
spread in frequencies
of a wave is decided by the
spread in frequencies
The waves are coherent for time delays 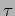 less than
less than 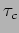 ie.
ie.
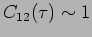 for
for 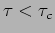 , and the waves are
incoherent for larger time delays ie.
, and the waves are
incoherent for larger time delays ie.
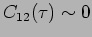 for
for
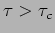 . Interference will be observed only if
. Interference will be observed only if 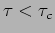 .
The coherence time can be converted to a
length-scale
.
The coherence time can be converted to a
length-scale 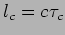 called the coherence length.
called the coherence length.
An estimate of the frequency spread
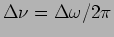 can be made by studying the intensity distribution of
a source with respect to frequency. Full width at half maximum
(FWHM) of the intensity profile gives a good estimate of the
frequency spread.
can be made by studying the intensity distribution of
a source with respect to frequency. Full width at half maximum
(FWHM) of the intensity profile gives a good estimate of the
frequency spread.
The Michelson interferometer can be used to measure the temporal
coherence 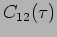 . Assuming that
. Assuming that 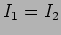 , we have
, we have
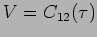 . Measuring the visibility of the fringes varying
. Measuring the visibility of the fringes varying
 the difference in the arm lengths of a Michelson
interferometer gives an estimate of the temporal coherence for
the difference in the arm lengths of a Michelson
interferometer gives an estimate of the temporal coherence for
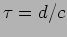 . The fringes will have a good contrast
. The fringes will have a good contrast 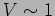 only
for
only
for 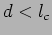 . The fringes will be washed away for
. The fringes will be washed away for  values
larger than
values
larger than 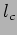 .
.
Problems
- Consider a situation where Young's double slit experiment is
performed using light of wavelength
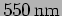 and
and
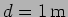 . Calculate the visibility assuming a source of angular
width
. Calculate the visibility assuming a source of angular
width 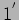 and . Plot
and . Plot 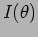 for both these
cases.
for both these
cases.
- A small aperture of diameter
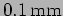 at a distance of
at a distance of
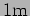 is used to illuminate two slits with light of wavelength
is used to illuminate two slits with light of wavelength
 . The slit separation is
. The slit separation is
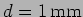 . What is the fringe spacing and the expected visibility of the
fringe pattern? (
. What is the fringe spacing and the expected visibility of the
fringe pattern? (
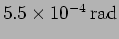 ,
, 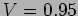 )
)
- A source of unknown angular extent
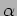 emitting light at
emitting light at
 is used in a Young's
double slit experiment where the slit spacing
is used in a Young's
double slit experiment where the slit spacing  can be varied. The
visibility is measured for different values of
can be varied. The
visibility is measured for different values of  . It is found
that the fringes vanish
. It is found
that the fringes vanish 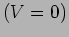 for
for
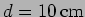 . [a.] What is
the angular extent of the source? (
. [a.] What is
the angular extent of the source? (
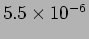 )
)
- Estimate the coherence time
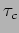 and coherence length
and coherence length
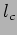 for the following sources
for the following sources
| Source |
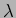 nm nm |
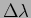 nm nm |
| White light |
550 |
300 |
| Mercury arc |
546.1 |
1.0 |
| Argon ion gas laser |
488 |
0.06 |
| Red Cadmium |
643.847 |
0.0007 |
| Solid state laser |
785 |
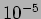 |
| He-Ne laser |
632.8 |
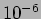 |
- Assume that Kr
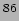 discharge lamp has roughly the
following intensity distribution at various wavelengths,
discharge lamp has roughly the
following intensity distribution at various wavelengths, 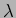 (in
(in 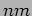 ),
),
Estimate the coherence length of Kr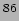 source.(Ans. 0.3m)
source.(Ans. 0.3m)
- An ideal Young's double slit (i.e. identical slits with
negligible slit width) is illuminated with a source having two
wavelengths,
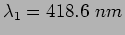 and
and
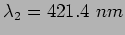 . The
intensity at
. The
intensity at 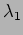 is double of that at
is double of that at 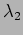 .
.
a) Compare the visibility of fringes near order 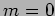 and near
order
and near
order 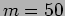 on the screen [visibility =
on the screen [visibility =
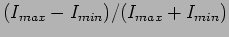 ].(Ans. 1:0.5)
].(Ans. 1:0.5)
b) At what order(s) on the screen visibility of the fringes is
poorest and what is this minimum value of the visibility. (Ans.
75, 225 etc. and 1/3)
- An ideal Young's double slit (separation
 between the
slits) is illuminated with two identical strong monochromatic
point sources of wavelength
between the
slits) is illuminated with two identical strong monochromatic
point sources of wavelength 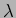 . The sources are placed
symmetrically and far away from the double slit. The angular
separation of the sources from the mid point of the double slit is
. The sources are placed
symmetrically and far away from the double slit. The angular
separation of the sources from the mid point of the double slit is
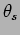 . Estimate
. Estimate 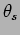 so that the visibility of the
fringes on the screen is zero. Can one have visibility almost 1
for a non zero
so that the visibility of the
fringes on the screen is zero. Can one have visibility almost 1
for a non zero 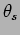 .
.
Hint: See the following figure 11.5,
Figure 11.5:
Two source
vanishing visibility condition
|
(Further reading: Michelson's stellar interferometer for
estimating angular separation of double stars and diameters of
distant stars)




Next: Diffraction
Up: Coherence
Previous: Spatial Coherence
Contents
Physics 1st Year
2009-01-06
![$\displaystyle \frac{1}{2} \langle [\tilde{E}_1(t)+\tilde{E}_2(t+\tau)] \, [\tilde{E}_1(t)+\tilde{E}_2(t+\tau)]^*
\rangle$](img891.png)
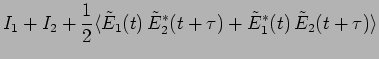
![$\displaystyle \frac{1}{2} \langle [\tilde{E}_1(t)+\tilde{E}_2(t+\tau)] \, [\tilde{E}_1(t)+\tilde{E}_2(t+\tau)]^*
\rangle$](img891.png)
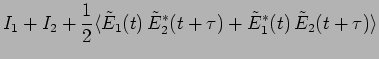
![]() and
and
![]() with
with
![]()
![]() and phase
and phase ![]() of the complex
amplitude
of the complex
amplitude ![]() both vary slowly with timescale T.
Figure 11.4 shows a situation where
both vary slowly with timescale T.
Figure 11.4 shows a situation where
![]() , a pure sinusoidal wave of the same frequency
is shown for comparison. What happens to eq. (11.10) in
the presence of a finite spread in frequencies? It now gets
modified to
, a pure sinusoidal wave of the same frequency
is shown for comparison. What happens to eq. (11.10) in
the presence of a finite spread in frequencies? It now gets
modified to
![]() can be made by studying the intensity distribution of
a source with respect to frequency. Full width at half maximum
(FWHM) of the intensity profile gives a good estimate of the
frequency spread.
can be made by studying the intensity distribution of
a source with respect to frequency. Full width at half maximum
(FWHM) of the intensity profile gives a good estimate of the
frequency spread.
![]() . Assuming that
. Assuming that ![]() , we have
, we have
![]() . Measuring the visibility of the fringes varying
. Measuring the visibility of the fringes varying
![]() the difference in the arm lengths of a Michelson
interferometer gives an estimate of the temporal coherence for
the difference in the arm lengths of a Michelson
interferometer gives an estimate of the temporal coherence for
![]() . The fringes will have a good contrast
. The fringes will have a good contrast ![]() only
for
only
for ![]() . The fringes will be washed away for
. The fringes will be washed away for ![]() values
larger than
values
larger than ![]() .
.
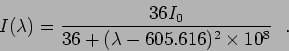
![]() and near
order
and near
order ![]() on the screen [visibility =
on the screen [visibility =
![]() ].(Ans. 1:0.5)
].(Ans. 1:0.5)