



Next: Temporal Coherence
Up: Coherence
Previous: Coherence
Contents
The Young's double slit experiment (Figure 11.1)
essentially measures the spatial coherence. The wave 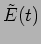 at
the point P on the screen is the superposition of
at
the point P on the screen is the superposition of
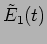 and
and
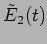 the contributions from slits
the contributions from slits  and
and 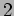 respectively.
Let us now shift our attention to the values of the electric field
respectively.
Let us now shift our attention to the values of the electric field
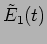 and
and
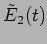 at the positions of the two slits. We
define the spatial coherence of the electric field at the two slit
positions as
at the positions of the two slits. We
define the spatial coherence of the electric field at the two slit
positions as
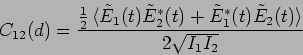 |
(11.1) |
Figure 11.1:
Young's double
slit with a point source
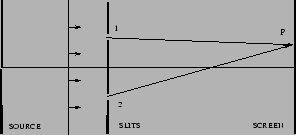 |
The waves from the two slits pick up different phases along the path
from the slits to the screen. The resulting intensity pattern on the
screen can be written as
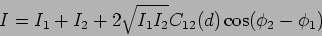 |
(11.2) |
where 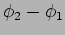 is the phase difference in the path
from the two slits to the screen. The term
is the phase difference in the path
from the two slits to the screen. The term
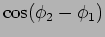 gives rise to a fringe pattern.
gives rise to a fringe pattern.
The fringe visibility defined as
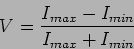 |
(11.3) |
quantifies the contrast of the fringes produced on the screen. It
has values in the range 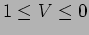 . A value
. A value 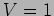 implies
very high contrast fringes, the fringes are washed away when
implies
very high contrast fringes, the fringes are washed away when
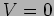 .
.
Figure 11.2:
Fringe
intensity for different visibilities
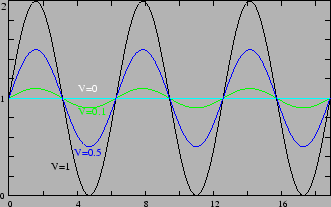 |
Figure 11.2 shows the fringe pattern for
different values of  . It can be easily checked that the visibility
is related to the spatial coherence as
. It can be easily checked that the visibility
is related to the spatial coherence as
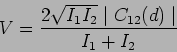 |
(11.4) |
and the visibility directly gives the spatial coherence
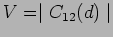 when
when 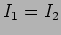 .
.
Let us first consider the situation when the two slits are
illuminated by a distant point source as shown in Figure
11.1. Here the two slits lie on the same wavefront, and
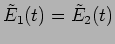 . We then have
. We then have
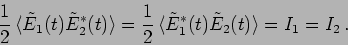 |
(11.5) |
whereby 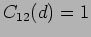 and the fringes have a visibility
and the fringes have a visibility 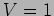 .
.
Figure 11.3:
Double slit
with a wide source
 |
We next consider the effect of a finite source
size. It is assumed that the source subtends an angle 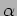 as
shown in Figure 11.3. This situation can be analyzed by
first considering a source at an angle
as
shown in Figure 11.3. This situation can be analyzed by
first considering a source at an angle 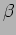 as shown in the
figure. This produces an intensity
as shown in the
figure. This produces an intensity
![\begin{displaymath}
I ( \theta, \beta)= 2 I_1 \left[ 1+ \cos \left( \frac{2 \pi d}{\lambda} (
\theta + \beta ) \right) \right]
\end{displaymath}](img882.png) |
(11.6) |
at a point at an angle 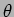 on the screen where it is assumed that
on the screen where it is assumed that
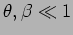 . Integrating
. Integrating 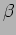 over the angular extent of the
source
over the angular extent of the
source
It is straightforward to calculate the spatial coherence
by comparing eq. (11.7) with eq. (11.2). This
has a value
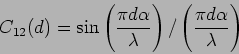 |
(11.8) |
and the visibility is
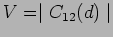 . Thus we see that
the visibility which quantifies the fringe contrast in the Young's
double slit experiment gives a direct estimate of the spatial
coherence. The visibility, or equivalently the spatial coherence
goes down if the angular extent of the source is increased. It is
interesting to note that the visibility becomes exactly zero when
the argument of the Sine term the expression (11.8)
becomes integral multiple of
. Thus we see that
the visibility which quantifies the fringe contrast in the Young's
double slit experiment gives a direct estimate of the spatial
coherence. The visibility, or equivalently the spatial coherence
goes down if the angular extent of the source is increased. It is
interesting to note that the visibility becomes exactly zero when
the argument of the Sine term the expression (11.8)
becomes integral multiple of 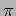 . So when the width of the
source is equal to
the visibility is
zero.
. So when the width of the
source is equal to
the visibility is
zero.
Why does the fringe contrast go down if the angular extent of the
source is increased? This occurs because the two slits are no
longer illuminated by a single wavefront, There now are many
different wavefronts incident on the slits, one from each point
on the source. As a consequence the electric fields at the two
slits are no longer perfectly coherent
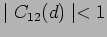 and the fringe contrast is reduced.
and the fringe contrast is reduced.
Expression (11.8) shows how the Young's double slit
experiment can be used to determine the angular extent of sources.
For example consider a situation where the experiment is done with
starlight. The variation of the visibility  or equivalently the
spatial coherence
or equivalently the
spatial coherence  with varying slit separation
with varying slit separation  is
governed by eq. (11.8). Measurements of the visibility
as a function of
is
governed by eq. (11.8). Measurements of the visibility
as a function of  can be used to determine
can be used to determine  the
angular extent of the star.
the
angular extent of the star.




Next: Temporal Coherence
Up: Coherence
Previous: Coherence
Contents
Physics 1st Year
2009-01-06
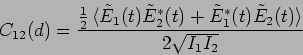
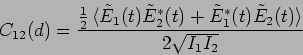
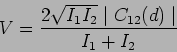
![]() . We then have
. We then have
![\begin{displaymath}
I ( \theta, \beta)= 2 I_1 \left[ 1+ \cos \left( \frac{2 \pi d}{\lambda} (
\theta + \beta ) \right) \right]
\end{displaymath}](img882.png)
![]() and the fringe contrast is reduced.
and the fringe contrast is reduced.
![]() or equivalently the
spatial coherence
or equivalently the
spatial coherence ![]() with varying slit separation
with varying slit separation ![]() is
governed by eq. (11.8). Measurements of the visibility
as a function of
is
governed by eq. (11.8). Measurements of the visibility
as a function of ![]() can be used to determine
can be used to determine ![]() the
angular extent of the star.
the
angular extent of the star.