



Next: The Spectrum of Electromagnetic
Up: The vector nature of
Previous: Circular polarization
Contents
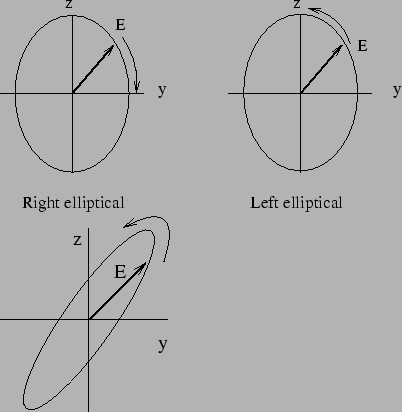
Oscillations of different amplitude combined with a phase difference
of 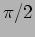 produces elliptically polarized wave where the ellipse
is aligned with the
produces elliptically polarized wave where the ellipse
is aligned with the 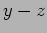 axis as shown in Figure
19.4. The ellipse is not aligned with the
axis as shown in Figure
19.4. The ellipse is not aligned with the 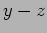 axis for an
arbitrary phase difference between the
axis for an
arbitrary phase difference between the 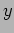 and
and 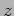 components of the electric
field. This is the most general state of
polarization shown in the last diagram of the Figure 19.4. Linear and
circularly polarized waves are specific cases of elliptically polarized waves.
components of the electric
field. This is the most general state of
polarization shown in the last diagram of the Figure 19.4. Linear and
circularly polarized waves are specific cases of elliptically polarized waves.
Figure 8.4:
Elliptical plarization
 |
Problems
- Find the plane of polarization of a light which is moving in the positive
 direction and having amplitudes of electric field in the
direction and having amplitudes of electric field in the 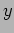 and
and 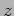 directions,
directions, 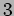 and
and 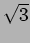 respectively in same units. The oscillating
components of the electric field along
respectively in same units. The oscillating
components of the electric field along 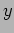 and
and 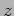 have the same frequency and
wavelength and the
have the same frequency and
wavelength and the 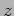 component is leading with a phase
component is leading with a phase 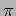 .
.
- Find the state of polarization of a light which is moving in the positive
 direction with electric field amplitudes same along the
direction with electric field amplitudes same along the 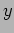 and
and 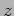 directions.
The oscillating components of the electric field along the
directions.
The oscillating components of the electric field along the 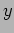 and
and 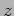 have the
same frequency and wavelength and the
have the
same frequency and wavelength and the 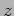 component is lagging with a phase
component is lagging with a phase
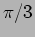 .
.
(Ans: Left elliptically polarized and the major axis is making an angle
with the 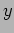 axis.)
axis.)
- Find the state of polarization of a light which is moving in the positive
 direction and having amplitudes of electric field in the
direction and having amplitudes of electric field in the 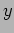 and
and 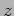 directions,
directions,
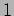 and
and 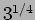 respectively in same units. The oscillating components of the
electric field along
respectively in same units. The oscillating components of the
electric field along 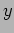 and
and 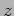 have the same frequency and wavelength and the
have the same frequency and wavelength and the
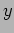 component is leading with a phase
component is leading with a phase 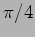 .
.
(Ans: Left elliptically polarized and the major axis is making an angle
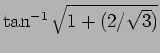 with the
with the 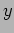 axis.)
axis.)
- Find out the maximum and minimum values of electric field at point
 for the previous problem.
(Ans:
for the previous problem.
(Ans:
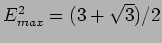 and
and
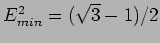 .)
.)




Next: The Spectrum of Electromagnetic
Up: The vector nature of
Previous: Circular polarization
Contents
Physics 1st Year
2009-01-06

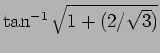 with the
with the