Complementary function and particular integral

The solution is a sum of two parts

$$\tilde{x}(t)=\tilde{A} e^{i \omega_0 t}+ \tilde{B} e^{i \omega t} \,.$$ (3.5)

The first term $\tilde{A} e^{i \omega_0 t}$, called the complementary function, is a solution to equation (3.4) without the external force. This oscillates at the natural frequency of the oscillator $\omega_0$. This part of the solution is exactly the same as when there is no external force. This has been discussed extensively earlier, and we shall ignore this term in the rest of this chapter.

The second term $\tilde{B} e^{i \omega t}$, called the particular integral, is the extra ingredient in the solution due to the external force. This oscillates at the frequency of the external force $\omega$. The amplitude $\tilde{B}$ is determined from equation (3.4) which gives

$$[-\omega^2 + \omega_0^2]\tilde{B}=\tilde{f}$$ (3.6)

whereby we have the solution

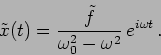$$\tilde{x}(t)=\frac{\tilde{f}}{\omega_0^2 - \omega^2} \, e^{i \omega t} \,.$$ (3.7)

The amplitude and phase of the oscillation both depend on the forcing frequency $\omega$. The amplitude is

$$\mid \tilde{x}\mid = \frac{f}{\mid \omega_0^2-\omega^2\mid} \,.$$ (3.8)

and the phase of the oscillations relative to the applied force is $\phi=0$ for and $\phi=-\pi$ for $\omega > \omega_0$.

Note: One cannot decide here whether the oscillations lag or lead the driving force, i.e. whether $\phi=-\pi$ or $\phi=\pi$ as both of them are consistent with $\omega > \omega_0$ case ( $e^{\pm i\pi}=-1$). The zero resistance limit, $\beta\rightarrow % 0$, of the damped forced oscillations (which is to be done in the next section) would settle it for $\phi=-\pi$ for $\omega > \omega_0$. So in this case there is an abrupt change of $-\pi$ radians in the phase as the forcing frequency, $\omega$, crosses the natural frequency, $\omega_0$.

Figure 3.1: Amplitue and phase as a function of forcing frequncy

The amplitude and phase are shown in Figure 3.1. The first point to note is that the amplitude increases dramatically as $\omega \rightarrow \omega_0$ and the amplitude blows up at $\omega=\omega_0$. This is the phenomenon of resonance. The response of the oscillator is maximum when the frequency of the external force matches the natural frequency of the oscillator. In a real situation the amplitude is regulated by the presence of damping which ensures that it does not blow up to infinity at $\omega=\omega_0$.

We next consider the low frequency $\omega \ll \omega_0$ behaviour

$$\tilde{x}(t) = \frac{\tilde{f}}{\omega_0^2} e^{i \omega t}=\frac{F}{k} e^{i( \omega t+\phi)}\,,$$ (3.9)

The oscillations have an amplitude and are in phase with the external force.

This behaviour is easy to understand if we consider which is a constant force. We know that the spring gets extended (or contracted) by an amount $x=F/k$ in the direction of the force. The same behaviour goes through if $F$ varies very slowly with time. The behaviour is solely determined by the spring constant $k$ and this is referred to as the ``Stiffness Controlled'' regime.

At high frequencies $\omega \gg \omega_0$

the amplitude is $F/m$ and the oscillations are $-\pi$ out of phase with respect to the force. This is the ``Mass Controlled'' regime where the spring does not come into the picture at all. It is straight forward to verify that equation (3.10) is a solution to

$$m \ddot{x}= F e^{i( \omega t+\phi)}$$ (3.11)

when the spring is removed from the oscillator. Interestingly such a particle moves exactly out of phase relative to the applied force. The particle moves to the left when the force acts to the right and vice versa.