Assignment II
Integration (Application)

We consider the 1-dimensional motion of a particle of mass $m$ in a time independent potential $V(x)$. The fact that the energy $E$ will be conserved allows us to integrate the equation of motion and obtain a solution in a closed form

$$t-C=\sqrt{\frac{m}{2}} \int_{x_i}^{x} \frac{d x^{'}}{\sqrt{E-V(x^{'})}} .$$

where for the choice $C=0$ the particle is at the position $x_i$ at the time $t=0$ and $x$ refers to its position at any arbitrary time $t$.

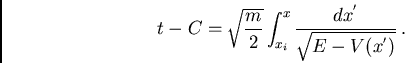
We consider a particular case where the particle is in bound motion between two points $a$ and $b$ where $V(a)=E$ and $V(b)=E$ and $V(x)<E$ for $a<x <b$. The time period of the oscillation $T$ is given by

$$T=2 \sqrt{\frac{m}{2}} \int_{xa}^{b} \frac{d x^{'}}{\sqrt{E-V(x^{'})}} .$$

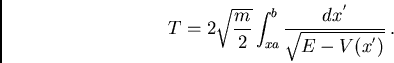
First consider a particle with $m=1 {\rm kg}$ in the potential $V(x)=(1/2) \alpha x^2$ with $\alpha=4 {\rm kg s^{-2}}$. Numerically calculate the time period of oscillation and check this againts the expected value. Verify that the frequency does not depend on the amplitude of oscillation.

Next consider a potential $V(x)=\exp((1/2) \alpha x^2)-1$. Numerically verify that for small amplitude oscillations you recover the same results as the simple harmonic oscillator. The time period is expected to be different for large amplitude oscillations. How does the time period vary with the amplitude of oscillations? Show this graphically.