



Next: LC Oscillator
Up: Why study the SHO?
Previous: Why study the SHO?
Contents
Figure 1.7:
(a) and (b)
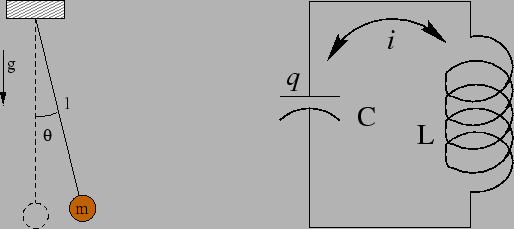 |
The simple possible shown in Figure 1.7(a) is possibly familiar
to all of us. A mass  is suspended by a rigid rod of length
is suspended by a rigid rod of length 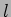 ,
the rod is assumed to be massless. The gravitations potential energy
of the mass is
,
the rod is assumed to be massless. The gravitations potential energy
of the mass is
![\begin{displaymath}
V(\theta)=m g l [1 - \cos \theta]\,.
\end{displaymath}](img88.png) |
(1.19) |
For small 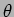 we may approximate
whereby the potential is
we may approximate
whereby the potential is
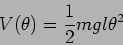 |
(1.20) |
which is the SHO potential. Here
gives the
torque not the force. The pendulum's equation of motion is
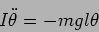 |
(1.21) |
where 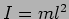 is the moment of inertia. This can be written as
is the moment of inertia. This can be written as
which allows us to determine the angular frequency
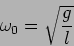 |
(1.23) |




Next: LC Oscillator
Up: Why study the SHO?
Previous: Why study the SHO?
Contents
Physics 1st Year
2009-01-06

![]() we may approximate
whereby the potential is
we may approximate
whereby the potential is