



Next: Phase velocity.
Up: Sinusoidal Waves.
Previous: What is ?
Contents
The sinusoidal wave in equation (6.2) has a complex
amplitude
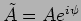 . Here
. Here 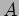 , the magnitude of
, the magnitude of 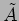 determines the magnitude of the wave. We refer to
determines the magnitude of the wave. We refer to
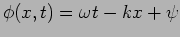 as the phase of the wave, and the wave can be also
expressed as
as the phase of the wave, and the wave can be also
expressed as
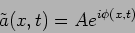 |
(6.3) |
If we study the behaviour of the wave at a fixed position 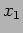 , we
have
, we
have
![\begin{displaymath}
\tilde{a}(t)=[\tilde{A}e^{-i kx_1}] e^{i \omega t}=\tilde{A}' e^{i \omega t}\,.
\end{displaymath}](img468.png) |
(6.4) |
We see that this is the familiar oscillation (SHO) discussed in detail
in Chapter 1. The oscillation has amplitude
![$\tilde{A}'=[\tilde{A}e^{- i k x_1}]$](img469.png) which includes an extra constant phase factor. The value of
has sinusoidal variations. Starting at
which includes an extra constant phase factor. The value of
has sinusoidal variations. Starting at 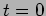 , the behaviour repeats
after a time period
, the behaviour repeats
after a time period 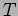 when
when
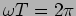 . We identify
. We identify 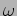 as
the angular frequency of the wave related to the frequency
as
the angular frequency of the wave related to the frequency 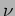 as
as
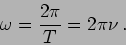 |
(6.5) |
We next study the wave as a function of position  at a fixed
instant of time
at a fixed
instant of time 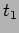 . We have
. We have
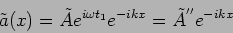 |
(6.6) |
where we have absorbed the extra phase
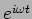 in the complex
amplitude
in the complex
amplitude
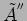 . This tells us that the spatial variation is
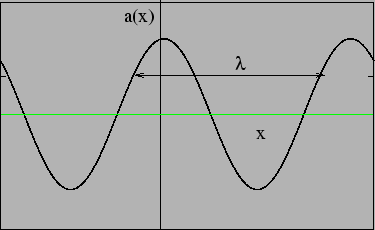
also sinusoidal as shown in Figure 6.2. The wavelength
. This tells us that the spatial variation is
also sinusoidal as shown in Figure 6.2. The wavelength
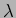 is the distance after which repeats
itself. Starting from
is the distance after which repeats
itself. Starting from 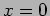 , we see that
, we see that 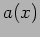 repeats when
repeats when 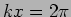 which tells us that
which tells us that
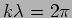 or
or
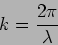 |
(6.7) |
where we refer to 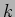 as the wave number. We note that the wave
number and the angular frequency tell us the rate of change of the
phase
as the wave number. We note that the wave
number and the angular frequency tell us the rate of change of the
phase 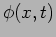 with position and time respectively
with position and time respectively
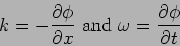 |
(6.8) |
Figure 6.2:
 |




Next: Phase velocity.
Up: Sinusoidal Waves.
Previous: What is ?
Contents
Physics 1st Year
2009-01-06
![]() , we
have
, we
have